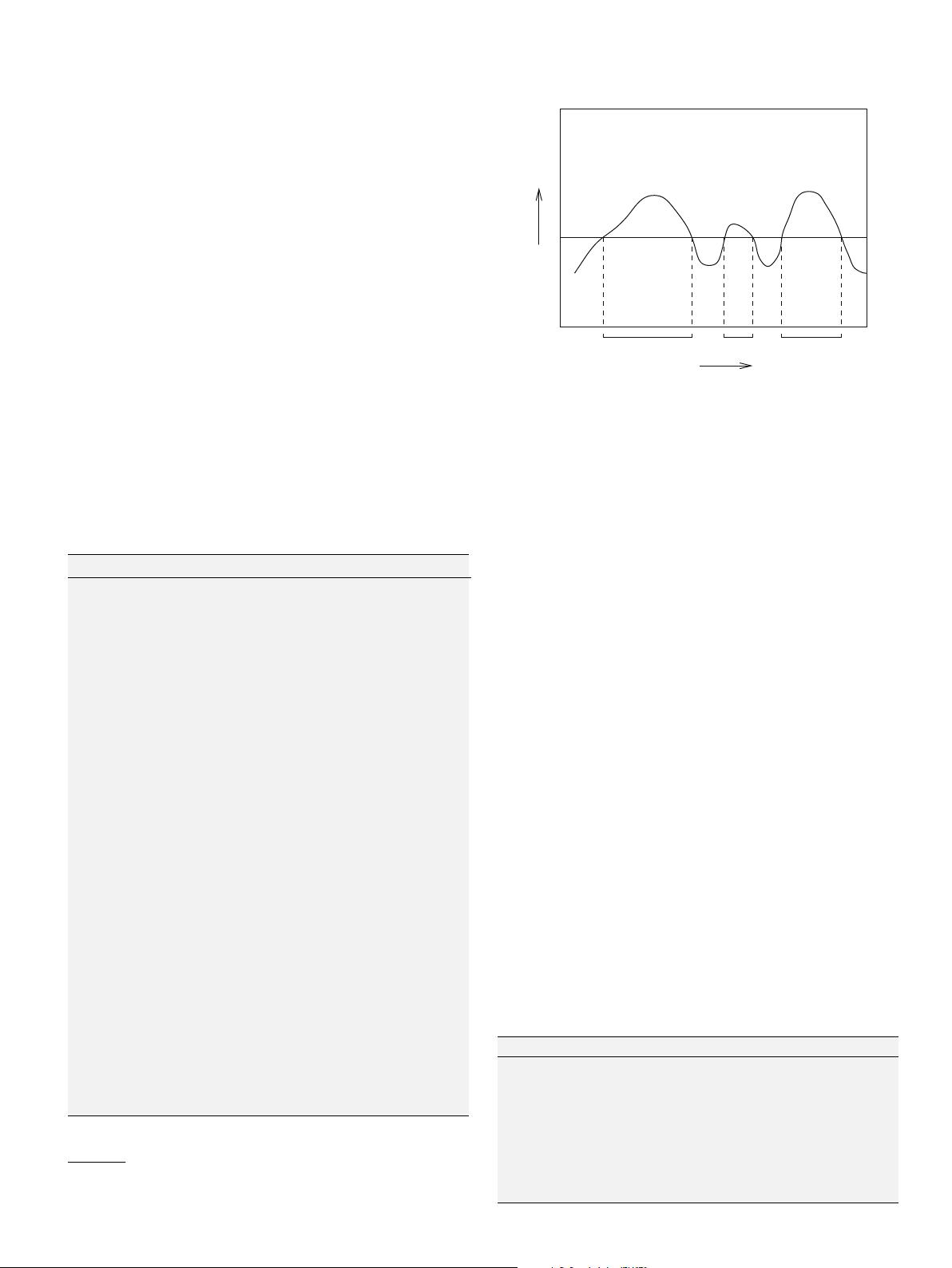
According to DBSCAN if a pattern x is dense
1
then it is part of a
cluster. A non-dense pattern can also be part of a cluster as a border
pattern of the cluster if it is at a distance less than or equal to
from
a dense pattern, otherwise it is a noisy outlier. Two patterns x
1
and
x
2
are in a cluster if there is a sequence of patterns x
1
; y
1
; y
2
; ...; y
m
; x
2
in the dataset such that:
(1) the distance between successive patterns in the sequence is
less than or equal to
,
(2) if m ¼ 0, then at least one of x
1
and x
2
is dense, and
(3) if m > 0, then the patterns y
1
; y
2
; ...; y
m
are dense.
The method DBSCAN is given in Algorithm 1 where D is the in-
put dataset, N
ðx; DÞ is the subset of patterns in D that are present
in the hyper-sphere of radius
at x where x 2 D. cardðN
ðx; DÞÞ is
the cardinality of the set which is nothing but jN
ðx; DÞj. For given
and MinPts, DBSCAN finds a dense point in the input set and ex-
pands it by merging neighboring dense regions together. The algo-
rithm marks each pattern of D with a cluster identifier (cid) which
gives the cluster to which the pattern belongs or gives a mark
‘‘noise” indicating that the pattern is a noisy one. One additional
mark ‘‘seen” is used to distinguish between the patterns which
are processed from that which are not. Note that a pattern which
is initially marked as ‘‘noise” can later become a border point of a
cluster and hence the ‘‘noise” mark can be deleted.
Algorithm 1. DBSCAN(D,
, MinPts)
{Each cluster is given an identifier cid}
cid =0;
for each pattern x in D do
if x is not marked as ‘‘seen” then
Mark x as ‘‘seen”;
Find N
ðx; DÞ;
if cardðN
ðx; DÞÞ <MinPts then
Mark x as ‘‘noise”;
else
Mark x as ‘‘seen”;
cid = cid +1;
Mark each pattern of N
ðx; DÞ with cluster
identifier cid;
Add each pattern of N
ðx; DÞ which is not marked
as ‘‘seen” to the list queue(cid).
while queue(cid) is not empty do
Take a pattern y from queue(cid) and mark it as
‘‘seen”;
if cardðN
ðy; DÞÞ >MinPts then
Mark each pattern of N
ðy; DÞ with cluster
identifier cid;
If any pattern of N
ðy; DÞ is marked as
‘‘noise” then remove this mark.
Add each pattern of N
ðy; DÞ which is not
marked as ‘‘seen” to the list queue(cid).
end if
Remove y from queue(cid).
end while
end if
end if
end for
Output all patterns of D along with their cid or ‘‘noise” mark;
It can be seen that the time consuming step in the DBSCAN is in
finding N
ðx; DÞ which can take OðnÞ time where x 2 D and jDj¼n.
Hence the time complexity of the method is Oðn
2
Þ. On the other-
hand, if we derive k leaders first by applying the leaders clustering
method and subsequently applying DBSCAN only with leaders has
a total time complexity of Oðn þ k
2
Þ. This is because the leaders
clustering method, as explained in subsequent sections, takes only
OðnÞ time to derive the leaders. Also it is formally established that
an upper-bound on the number of leaders i.e., k exists which is
independent of both n and the distribution from which the dataset
is drawn, provided the assumption that the data is drawn from a
bounded region of the feature space holds. Nevertheless, in gen-
eral, based on the experimental studies, it is shown that k is con-
siderably smaller than n, especially with large datasets. Hence
the hybrid scheme can be a faster one to work with large datasets.
Table 1 describes the space and time complexities of well known
clustering methods and rough-DBSCAN.
3. Leaders
In this section, we first present the leaders clustering method
(Spath, 1980; Hartigan, 1975) then as an improvement of this we
present the counted-leaders method which preserves the crucial
density information when the cluster representatives called leaders
are derived.
Leaders method finds a partition of the given dataset like most
of the clustering methods. Its primary advantage is its running
time which is linear in the size of the input dataset. To be more
precise, it can find the partition in OðnÞ time where n is the dataset
size. It needs to read (or scan) the dataset only once from the sec-
ondary memory and hence is also termed as an on-line clustering
method. Because of these factors the leaders method is gaining
Table 1
Time and space complexities of the well known clustering methods.
Method Time complexity Space complexity
Single/complete link
Oðn
3
Þ Oðn
2
Þ
K-means Oðn K tÞ OðKÞ
K-medians
Oðn
2
tÞ
OðnÞ
K-medoids (PAM)
OðK ðn KÞ
2
Þ
OðKÞ
DBSCAN
Oðn
2
Þ
OðnÞ
CURE
OðN
2
sample
Þ OðN
2
sample
Þ
BIRCH OðnÞ (2 database scans) OðN BÞ
Leader OðnÞ (1 database scan)
OðkÞ
Rough-DBSCAN
Oðn þ k
2
Þ (1 database scan)
OðkÞ
x
p(x)
CCC
123
T
Fig. 1. Clusters found by DBSCAN.
1
DBSCAN given in (Ester et al., 1996) calls a dense point as a core point and a non-
dense point as a non-core point. This modification is done to bring the material closer
to the pattern recognition community.
P. Viswanath, V. Suresh Babu / Pattern Recognition Letters 30 (2009) 1477–1488
1479









