信号处理指南：傅里叶变换特性

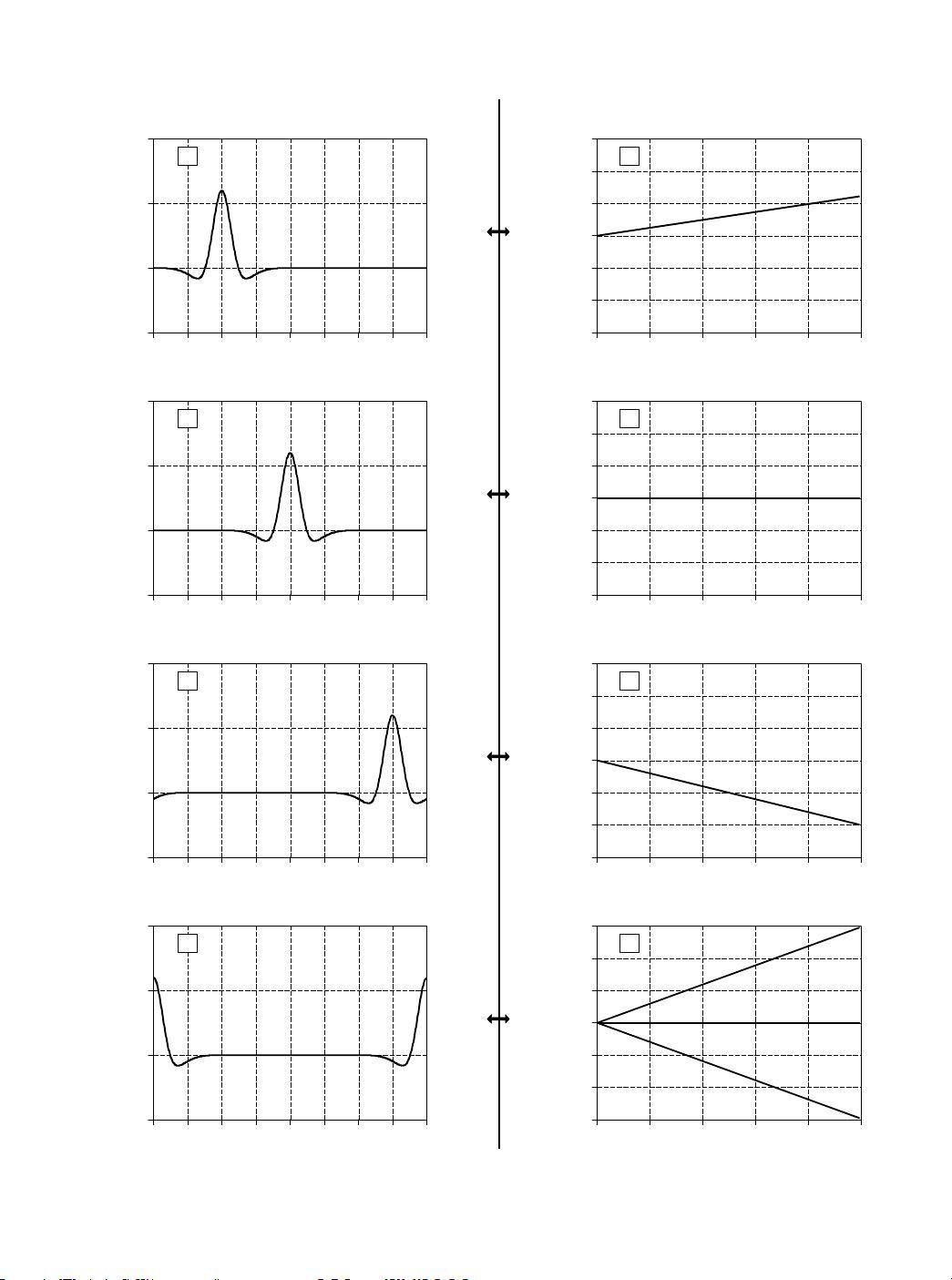
"The Scientist and Engineer's Guide to Digital Signal Processing -10: Chapter 10 Fourier Transform Properties" 在信号处理领域，傅里叶变换是连接时域与频域的关键工具，它揭示了这两种信号表示方式之间的数学关系。当信号在某一域内发生变化时，这种变化会在另一个域中以不同的形式体现出来。例如，上一章提到，时域信号的卷积会导致它们的频谱相乘。此外，加法、标度和移位等数学运算在对偶域中也有对应的运算，这些关系被称为傅里叶变换的性质。 线性性质 傅里叶变换具有线性性质，这包括齐次性和加性。这一特性适用于傅里叶变换家族的所有四个成员：傅里叶变换、傅里叶级数、离散傅里叶变换（DFT）和离散时间傅里叶变换（DTFT）。图10-1举例展示了齐次性是如何成为傅里叶变换的属性。图(a)显示了一个任意的时域信号，如果该信号乘以一个常数α，其傅里叶变换将相应地乘以相同的常数α，这是齐次性的表现。而加性则表明，两个时域信号的和在频域内对应于这两个信号频谱的简单相加。 尺度和移位性质 傅里叶变换还具有尺度和移位的性质。在时域中，信号向左或向右移动会导致频域内的相应变化。例如，将一个信号延迟τ单位时间，在频域内会得到该信号的复共轭乘以e^(-j2πfτ)，这称为时间平移定理。相反，如果信号被乘以一个时间函数，如e^(j2πft)，则在频域内会出现相应的空间平移。 共轭对称性和实信号 对于实信号，其傅里叶变换具有共轭对称性。这意味着如果x(t)是实信号，其傅里叶变换X(f)是共轭对称的，即X(-f) = X*(f)，其中*表示复共轭。这一性质在处理实信号时非常有用，因为它简化了频谱的表示和计算。 卷积和乘积性质 时域中的卷积对应于频域的乘积，反之亦然。这意味着两个信号x1(t)和x2(t)的卷积x1(t) * x2(t)在频域中表现为它们各自傅里叶变换的乘积X1(f)X2(f)。同样，时域内的乘积对应于频域的卷积，即x1(t)x2(t)的傅里叶变换为X1(f) * X2(f)。 傅里叶变换的逆变换 傅里叶变换还有一个重要的特性，即可逆性。每个傅里叶变换都有一个逆变换，可以将信号从频域转换回时域，反之亦然。逆傅里叶变换提供了在两个域之间转换信号的完整桥梁。 离散傅里叶变换与周期性 离散傅里叶变换（DFT）是傅里叶变换在离散时间信号上的应用，它处理的是有限长度的信号。DFT将周期性引入时域信号，因此在频域中得到的也是周期性的频谱。这在数字信号处理中尤其重要，因为它允许我们用有限的计算资源来处理无限信号的近似。 总结来说，傅里叶变换的这些性质是理解并应用数字信号处理的基础，它们不仅在理论分析中起着关键作用，而且在实际的信号处理算法设计中不可或缺。通过掌握这些性质，工程师和科学家能够有效地在时域和频域之间进行转换，从而优化信号处理任务，如滤波、压缩和通信系统的分析。