深度学习高效几何特征：ICCV 2017论文总结
需积分: 0 51 浏览量
更新于2024-08-26
收藏 8.12MB PDF 举报
"Learning Compact Geometric Features (ICCV 2017)是一篇探讨在无结构点云中学习局部几何特征的学术论文。该研究由Marc Khoury（加州大学伯克利分校）和Qian-Yi Zhou（英特尔实验室）以及Vladlen Koltun（英特尔实验室）共同完成。论文的核心关注点在于如何通过数据驱动的方法，利用深度学习技术来设计出既能精确又能保持紧凑性的局部特征，这些特征对于三维视觉和机器人技术中的几何配准至关重要。
当前，无结构点云的局部特征处理主要依赖于手工设计，这往往难以兼顾精确度、紧凑性和鲁棒性。作者提出了一种新的方法，即通过优化深度神经网络，将高维的局部点云分布转化为低维的欧式空间表示。这种方法的优点在于，它可以根据需求调整维度，生成一系列参数化的特征，从而超越现有描述符在性能上的限制。
1. 引言：
局部几何描述符的目标是捕捉点云中某一点周围的几何信息。在几何配准中，它们扮演着基础角色，这一过程支撑着机器人技术与三维视觉的广泛应用，如机器人导航、物体识别和场景重建等现代3D应用。
论文的主要贡献在于构建了一个学习型框架，能够自动学习并生成具有优良特性的几何特征，不仅精度更高，而且在紧凑性方面也有所提升。这对于在复杂、变化多端的环境中进行精确匹配和定位具有重要意义。通过深度学习的迭代训练，该模型能够逐渐适应不同场景下的几何特征提取，并且展现出更好的泛化能力。
这篇论文提供了一种创新的途径，挑战了传统的手动特征设计方法，展示了在无结构点云处理中利用机器学习提取高效、精确几何特征的可能性，为未来的三维数据处理技术开辟了新的研究方向。"
Learning Compact Geometric Features
Marc Khoury
UC Berkeley
Qian-Yi Zhou
Intel Labs
Vladlen Koltun
Intel Labs
Abstract
We present an approach to learning features that rep-
resent the local geometry around a point in an unstruc-
tured point cloud. Such features play a central role in ge-
ometric registration, which supports diverse applications
in robotics and 3D vision. Current state-of-the-art local
features for unstructured point clouds have been manually
crafted and none combines the desirable properties of pre-
cision, compactness, and robustness. We show that features
with these properties can be learned from data, by optimiz-
ing deep networks that map high-dimensional histograms
into low-dimensional Euclidean spaces. The presented ap-
proach yields a family of features, parameterized by dimen-
sion, that are both more compact and more accurate than
existing descriptors.
1. Introduction
Local geometric descriptors represent the local geome-
try around a point in a point cloud. They play a central role
in geometric registration, which supports diverse applica-
tions in robotics and 3D vision [16] and underpins modern
3D reconstruction pipelines [42]. To enable accurate and
efficient registration, the descriptor must possess a number
of properties [12]. First, it should map the local geometry
to a vector in a Euclidean space R
n
; such Euclidean repre-
sentations support efficient geometric search structures and
nearest-neighbor queries. Second, the descriptor should be
discriminative: nearest neighbors in feature space should
correspond to points with genuinely similar local neighbor-
hoods. Third, the representation should be compact, with
a small dimensionality n: this supports fast spatial search.
Finally, the representation should be robust to artifacts that
are commonly encountered in real data, such as noise and
missing regions.
The design of local geometric descriptors has been the
subject of intensive study for the past two decades. Many
hand-crafted descriptors have been designed and evalu-
ated [19, 11, 25, 27]. Nevertheless, no existing descriptor
jointly satisfies the desiderata of high discriminative abil-
ity, compactness, and robustness [12]. Part of the challenge
10
1
10
2
10
3
Dimensionality
0
10
20
30
40
50
60
Precision (%)
CGF-12
CGF-32
CGF
FPFH
PFH
RoPS
SHOT
SI
USC
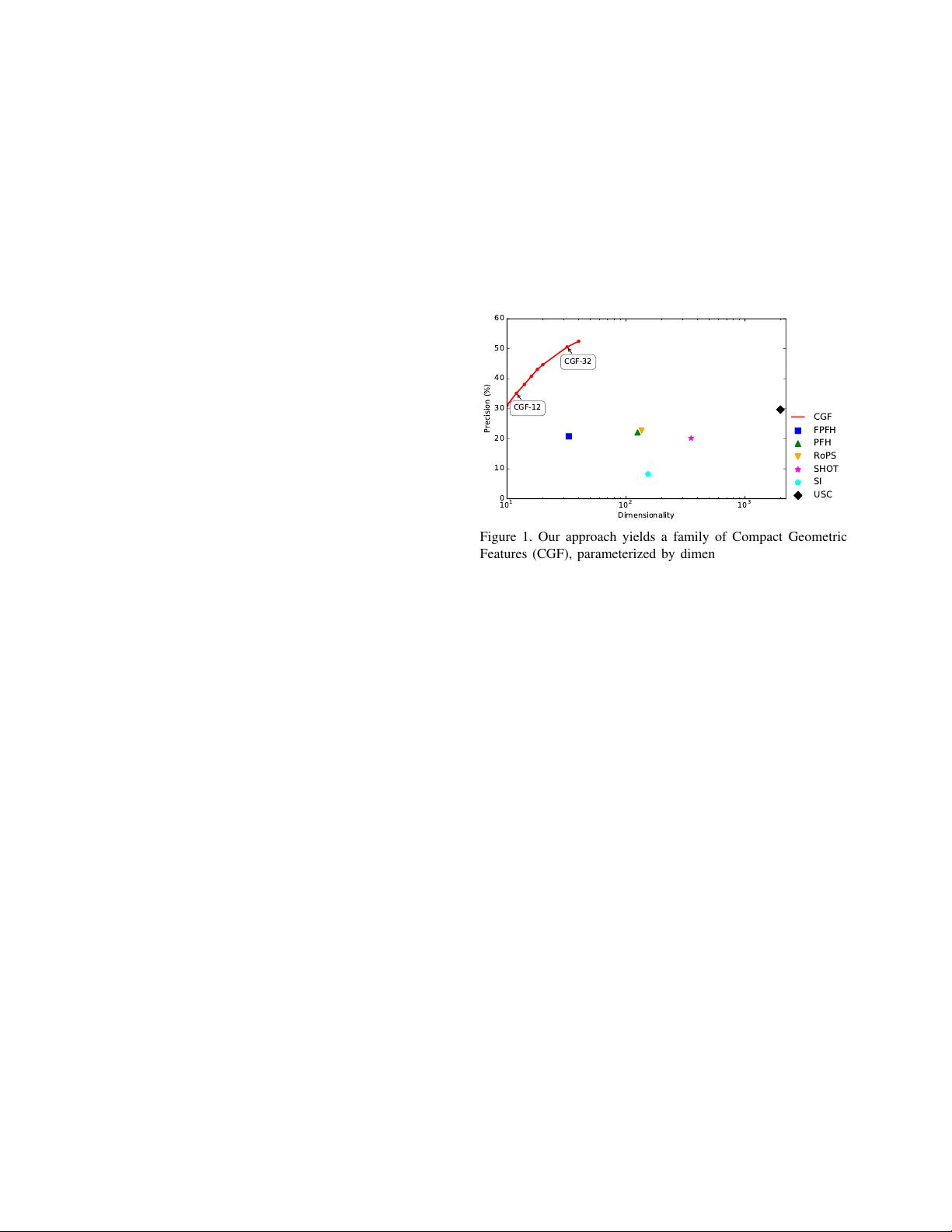
Figure 1. Our approach yields a family of Compact Geometric
Features (CGF), parameterized by dimension. This figure illus-
trates the performance of CGF on the SceneNN test set. Our fea-
tures are both more compact and more precise than the baselines.
The horizontal axis (dimensionality) is on a logarithmic scale.
is the difficulty of optimizing the parameters of a high-
dimensional feature representation by hand.
In this paper, we present an approach to learning local
geometric features from data. Our descriptor applies di-
rectly to unstructured point clouds and does not require a
clean and consistent surface parameterization [5], a vol-
umetric representation [41], or the synthesis of auxiliary
depth images [35]. Our features support nearest-neighbor
queries in a Euclidean space, which allows establishing
dense correspondences across point sets in near-linear time,
in contrast to the quadratic complexity required by pair-
wise matching networks. We thus obtain the first learned
geometric feature that can serve as a drop-in replace-
ment for state-of-the-art hand-crafted features in existing
pipelines [16, 42].
We show that the presented approach yields descrip-
tors that are both more discriminative and more compact
than state-of-the-art hand-crafted features. An illustration
is provided in Figure 1. Experiments demonstrate that our
Compact Geometric Features (CGF) yield more accurate
matches at lower query times. When CGF is used on the
standard Redwood benchmark for geometric registration,
with no training or fine-tuning on that dataset, it yields the
highest recall reported on the benchmark to date.
1
arXiv:1709.05056v1 [cs.CV] 15 Sep 2017
下载后可阅读完整内容，剩余8页未读，立即下载
小码1号
- 粉丝: 10
- 资源: 15
我的内容管理
展开
