WANG et al.: TOWARD THE PREDICTION LEVEL OF SITUATION AWARENESS 6953
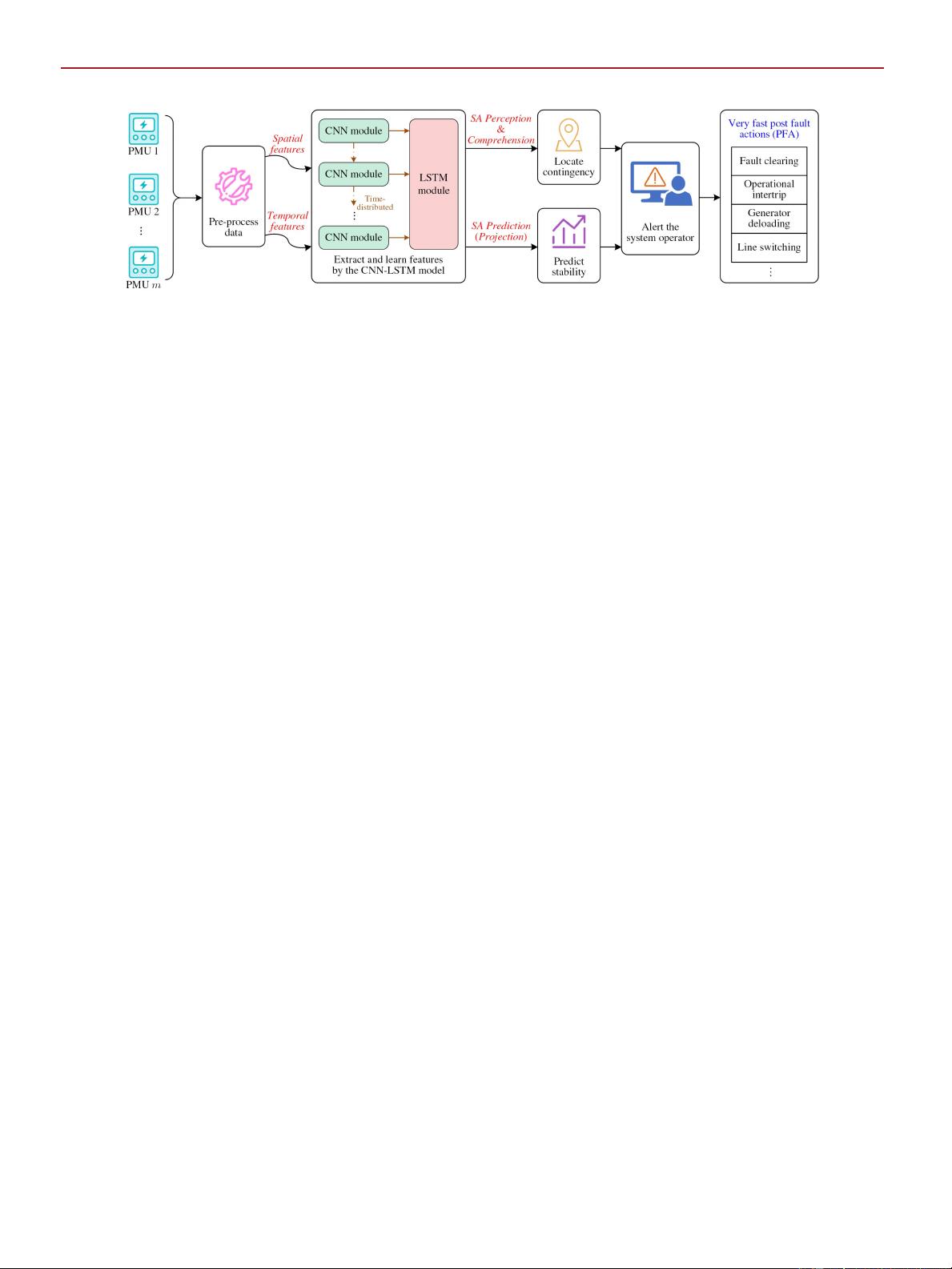
Fig. 1. Flowchart of the proposed SA model and its application.
the pixel-correlated arrays. The pooling layers (usually max
pooling) then merge those similar features in each feature
map [22]. RNN is another skillful model when processing
sequential data such as text and speech. RNN has a specialized
recurrent structure which can maintain memory over every time
step of the input sequence [23]. A variant of RNN, which is
known as LSTM network, has fixed the gradient vanishing or
exploding problems by a meticulously designed cell structure.
As a result, LSTM network has proved to be more powerful in
harnessing long-term memory [24].
The excellent performance of deep learning has facilitated a
number of data mining studies based on the wide-area PMU data.
Some of them utilized the spatial connectivity of the data [15],
[18], while others concentrated on the temporal correlation [14],
[16], [17]. However, few studies have made simultaneous min-
ing on both the spatial and temporal features. This will limit
the data mining ability of AI when dealing with the transient
stability prediction problems in power systems because power
system transient stability is a system-level issue which requires
exploration on the spatial connectivity, and at the same time
also a dynamic process which requires analysis on the temporal
correlation.
III. M
ETHODOLOGY
A. Framework Overview
The framework and workflow of the proposed SA model is
outlined in Fig. 1. First, all the measurement data from PMUs
are obtained and preprocessed to uncover the spatio-temporal
patterns inside the data. As the main body of the workflow,
the CNN-LSTM model is aggregated by two deep learning
modules—the CNN module and the LSTM module. The spatial
features within the data are extracted and learned by the CNN
module, while the temporal features are handled by the LSTM
module. The aggregation of these two modules is realized by a
time-distributed operation.
The CNN-LSTM model is designed to concurrently accom-
plish two tasks, i.e., contingency location and stability predic-
tion. By feeding a very short period of postfault data, the model
can not only locate the exact fault l ocation at present, but also
predict the stability status of the system in the future. In this
way, all three levels of SA (i.e., perception, comprehension, and
prediction) can be achieved. As for the field application, the
proposed SA model can alert the system operator in a prompt
and accurate manner, in order to implement very fast postfault
actions (PFA) subsequently.
B. Data Preprocessing
1) Matrix Mapping: As the first component of the CNN-
LSTM model, the CNN module requires the shape of input data
to be 2-D array-like. Therefore, it is necessary to map the 1-D
measurement data into the expected 2-D form. Some pioneer
studies have presented feasible solutions on the PMU data
preparation for the CNN model. For example, Gupta et al. [16]
proposed a novel operation to map the 1-D PMU data into a 2-D
heatmap representation, to facilitate the instability prediction
function of the CNN model. Inspired by [16], this article creates
an improved mapping operation named matrix mapping, to map
the 1-D measurement data (i.e., 1-D vector which consists of
all PMU measurements) into a 2-D measurement matrix. The
matrix mapping is operated as
X =[x
i,j
]
m×m
=
x
i,j
= 0 i = j
x
i,j
= a
i
− a
j
i = j
(1)
where X is the m × m measurement matrix, x
i,j
denotes every
entry of X for i = 1, 2,...,m, and j = 1, 2,...,m, m is the
total number of measurements. Besides, a
i
and a
j
are the
respective ith and jth measurement from the original vector
[a
1
,...,a
i
,...,a
j
,...,a
m
].
The matrix mapping uses a simple but effective way to obtain
the spatial relationships of every PMU measurement. These
spatial relationships are stored pairwise as every entry of the 2-D
measurement matrix. By representing the spatial r elationships,
the 2-D measurement matrix is filled with implicit spatial fea-
tures which are well prepared to be captured by the subsequent
CNN module. In addition, since the difference between two mea-
surements tends to be small, such matrix mapping is conducive
to form a uniform scale of the 2-D measurement matrix, which
adapts better to the shared weights property of CNN.
2) Label Encoding: Most of the deep learning models (in-
cluding the proposed CNN-LSTM model) require all input
variables and output variables to be numerical. However, the
label data are in fact categorical rather than numerical which
cannot be directly utilized as the output of the CNN-LSTM
model. Therefore, it is necessary to encode the label data into a
numerical form to fulfill the output requirements. To be specific
Authorized licensed use limited to: Wuhan University. Downloaded on July 04,2022 at 03:51:10 UTC from IEEE Xplore. Restrictions apply.
剩余10页未读，继续阅读
RachelMuZy
- 粉丝: 127
- 资源: 3
我的内容管理
展开
最新资源
- 解决Eclipse配置与导入Java工程常见问题
- 真空发生器：工作原理与抽吸性能分析
- 爱立信RBS6201开站流程详解
- 电脑开机声音解析：故障诊断指南
- JAVA实现贪吃蛇游戏
- 模糊神经网络实现与自学习能力探索
- PID型模糊神经网络控制器设计与学习算法
- 模糊神经网络在自适应PID控制器中的应用
- C++实现的学生成绩管理系统设计
- 802.1D STP 实现与优化：二层交换机中的生成树协议
- 解决Windows无法完成SD卡格式化的九种方法
- 软件测试方法：Beta与Alpha测试详解
- 软件测试周期详解：从需求分析到维护测试
- CMMI模型详解：软件企业能力提升的关键
- 移动Web开发框架选择：jQueryMobile、jQTouch、SenchaTouch对比
- Java程序设计试题与复习指南
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
