phase of the loop transfer function is flat at the gain
crossover frequency thereby guaranteeing the invariance
of the phase margin with respect to the process DC-gain
variation such as pay-load, amplifier feed forward gain
and the load current/resistance in power systems. On
the other hand through IMC strategy, the PID controller
is tuned by a single parameter unlike three parameters
in traditional PID controllers. Also, on the contrary to
the conventional fractional-order PID controllers which
require five parameters, the proposed scheme requires
only two tuning parameters. The tuning law is based on
the desired gain crossover frequency and phase margin.
The proposed scheme is verified experimentally on hard-
ware set-up of DC servomotor for speed control prob-
lem. It is observed that the dynamic properties of the
closed-loop with the proposed fractional-order control-
ler are better than that of the closed-loop with the inte-
ger-order controller. Moreover, the controller brings
optimality in terms of integral error specification. The
proposed scheme is further extended to position control
problem and validated on QUBE-Servo 2 set up.
The other contribution in this paper comes in the form of
evaluation of the robustness of the control loop. We
know that the CRONE control principle yields robustness
against plant perturbation but the limit of the plant
uncertainty is not directly evaluated through this method.
To fulfill this gap, we have derived the condition which
provides the limit of uncertainty in the plant gain varia-
tion to maintain the robust performance of controller.
2. PROBLEM FORMULATION
The armature controlled DC servomotor model, as
shown in Figure 1, has been studied by many authors, to
analyse and optimize its functionality. Its linearized elec-
tromechanical dynamics
1
can be described as
d
dt
i
a
¼
R
L
i
a
K
b
L
v þ
1
L
u (1)
d
dt
v ¼
d
J
v þ
K
t
J
i
a
(2)
where i
a
is the armature winding current, v is the rotor
angular speed, R is the armature winding resistance, L is
the armature winding inductance, K
b
is the back electro-
motive force constant, u is the armature winding input
voltage, K
t
is the torque constant, J is the system moment
of inertia, and d is the system damping coefficient. From
(1) and (2), the DC motor can be expressed in a linear
time invariant and single-input single-output (SISO)
system and can be described by a rational proper trans-
fer function:
PsðÞ¼
v sðÞ
usðÞ
¼
K
t
JLs
2
þ JR þ dLðÞs þ dR þ K
b
K
t
ðÞ
In PMS set-up, an additional conversion gain h is
commissioned with
PsðÞ. Therefore, the complete model
can now be written as:
Ps
ðÞ
¼
K
JLs
2
þ JR þ dLðÞs þ dR þ K
b
K
t
ðÞ
(3)
where K = hK
t
. Here, our objective is to provide a syn-
thesis method to design a controller C(s) in a feedback
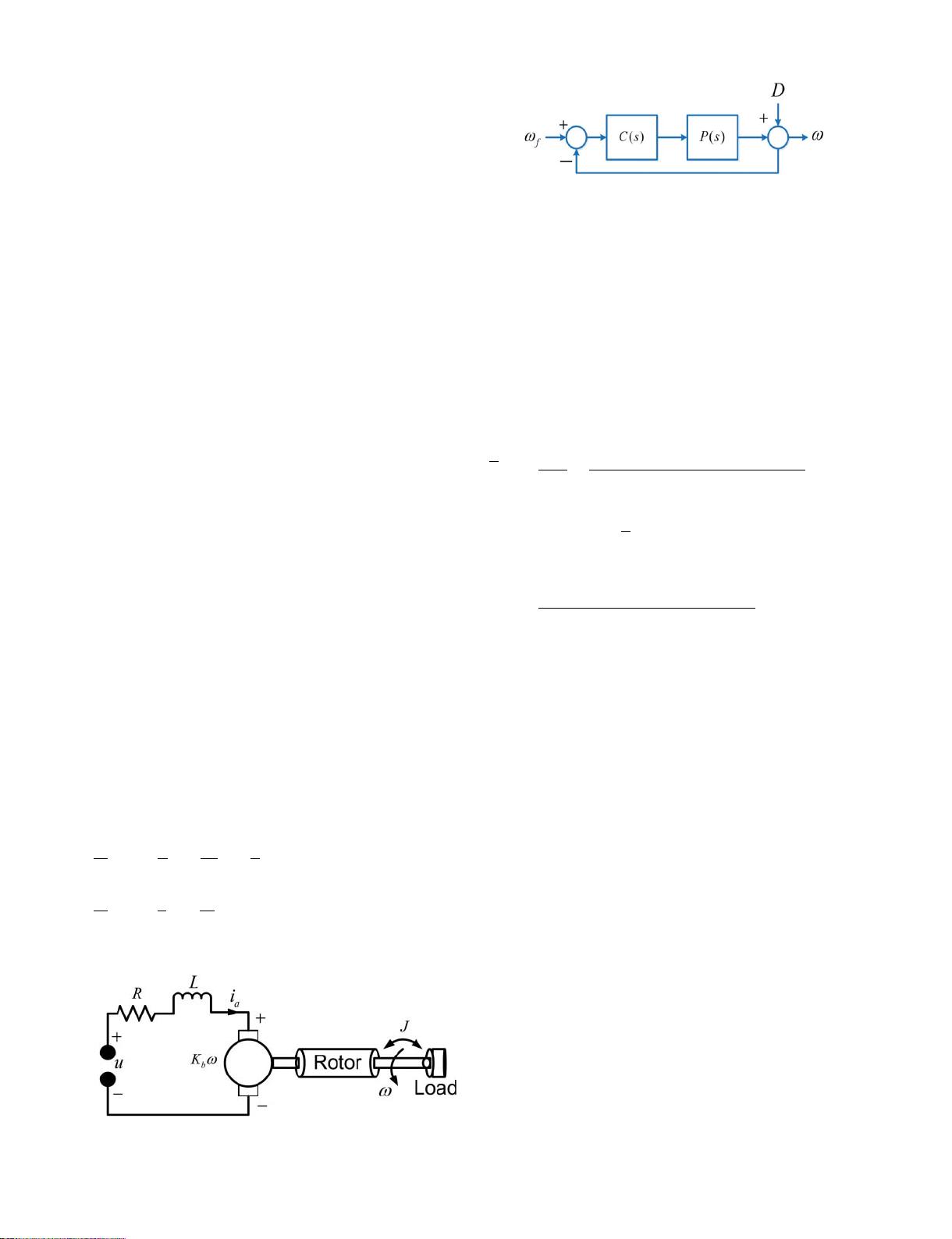
configuration (see Figure 2) such that the DC motor
tracks the reference speed without steady-state error and
meets specified control performance. Thus, it is a track-
ing problem in which we need lim
t !1
v tðÞ¼v
f
for
all D where D is disturbance.
3. THEORETICAL BACKGROUND FOR
CONTROLLER DESIGN
In this section, we present and analyse some principles
that characterize and help in formulating the controller.
3.1 Fractional-Order System
The fractional calculus is a generalization of integration
and derivation to non-integer order operators. The con-
cept of fractional-order mathematics and system were
planted over 300 years ago, however its potential appli-
cations are traced out from past two decades [33–36].
These days in control system design, the fractional-order
based strategy has become an active field of research but
still it is in initial phase and many aspects are yet to be
Figure 1: Schematic of DC servomotor model
Figure 2: Unity feedback configuration
50 S. SAXENA AND Y. V. HOTE: DESIGN AND VALIDATION OF FRACTIONAL-ORDER CONTROL SCHEME









