位运算轻松掌握：从二进制到十六进制

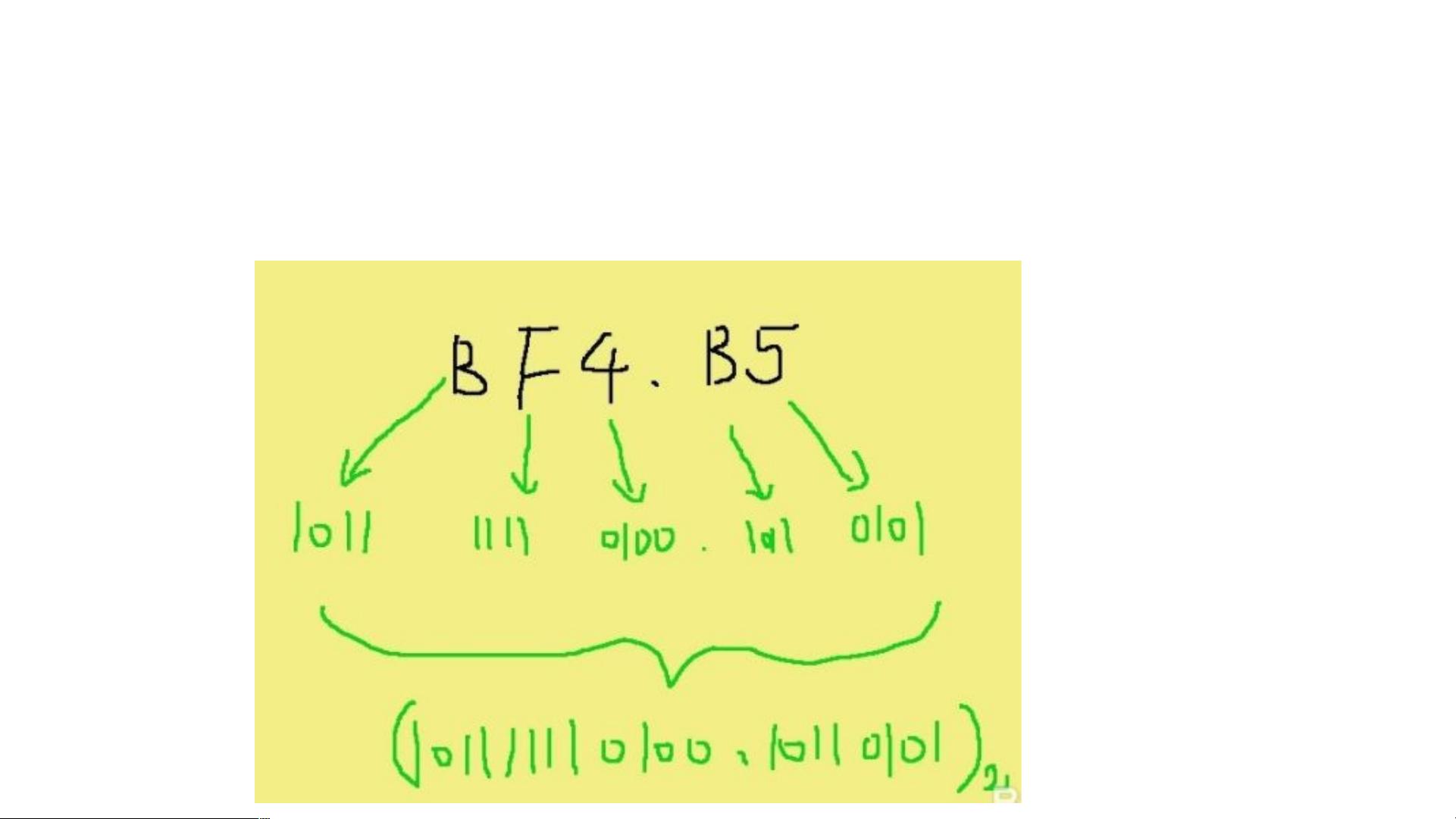
"位运算快入门的PPT涵盖了从进制转换到位运算的各种基础知识，旨在简化学习过程，包括二进制与十六进制之间的转换、位运算的常见技巧，如按位与、按位或、按位异或等操作。" 在计算机科学中，位运算是对数据在内存中的二进制形式进行直接操作的关键工具。了解并熟练掌握位运算对于编程和系统级设计至关重要。首先，我们需要理解不同进制之间的转换，特别是二进制和十六进制之间的转换。 十六进制（Hexadecimal）是一种方便人类使用的逢16进1的进位计数制，它使用0-9的阿拉伯数字和A-F的字母来表示从0到15的数值。在表示十六进制数时，我们通常会在后面加上字母'H'或者使用'0x'作为前缀。例如，'BH'代表11（十进制），而'0X23'则表示23（十进制）。 二进制和十六进制之间的转换关系是基于这样的事实：每个十六进制数字对应四位二进制数。因此，16进制的1对应二进制的0001，2对应0010，直到F对应1111。在转换过程中，确保二进制数的位数是4的倍数是很重要的。不足四位时，可以在左侧补零。同样，将十六进制转换为二进制时，我们需要将每个十六进制位拆分为四个二进制位，并进行相应的权重累加。 接下来，我们讨论位运算。位运算直接作用于整数的二进制位，包括以下几种常见类型： 1. 按位与（AND）运算：两个数的每一位进行逻辑与运算，只有当对应的两位都是1时，结果的对应位才为1。例如，6（110）与11（1011）进行AND运算得到2（0010）。此运算常用于二进制取位操作，例如通过一个数与1进行AND运算，我们可以快速确定该数是否为偶数（最末位为0）。 2. 按位或（OR）运算：对于两个数的每一位，只要有一个为1，结果的对应位就为1。例如，将一个数与1进行OR运算，可以将二进制的最末位强行设置为1，若需要将最末位设为0，可以先OR再减1，使得末位翻转后变为0。 3. 按位异或（XOR）运算：当两个对应的二进制位不相同时，结果的对应位为1。异或运算常用于不改变某些特定位而改变其他位的操作，或者检查两个数是否相等（异或结果为0）。 位运算在计算机科学中扮演着重要角色，它们在内存管理、数据编码、优化算法等方面都有广泛应用。熟悉和精通位运算，可以提高代码效率，解决一些底层问题，是成为优秀程序员的必备技能之一。通过深入学习和实践，你可以更有效地理解和运用这些概念，从而提升编程能力。