提高精度的Runge-Kutta方法：解决常微分方程的第四阶算法

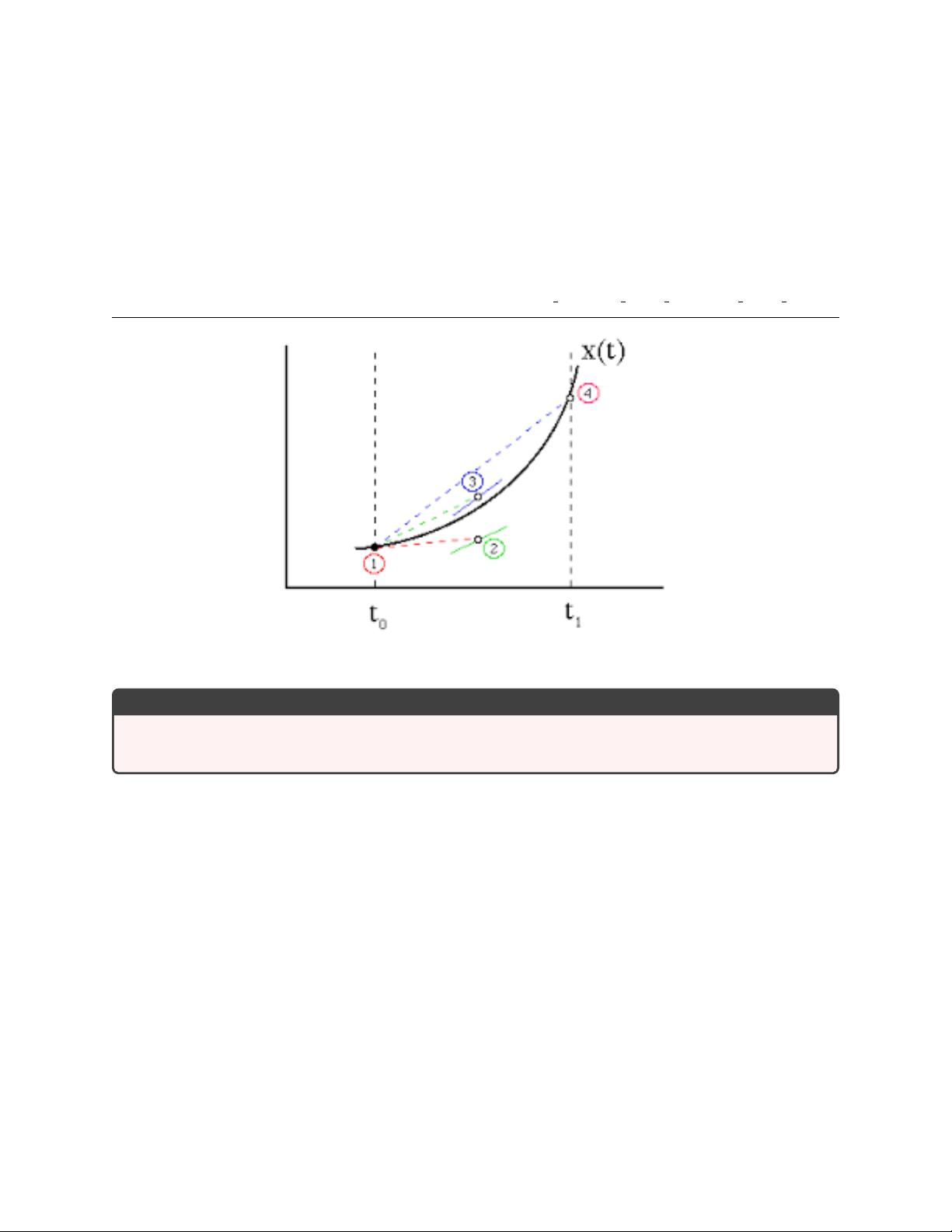
在《odes_runge_kutta.pdf》一文中，讨论了常微分方程(ODE)的数值解法，特别是Runge-Kutta方法。这些方法相较于欧拉方法更精确，尤其在处理复杂非线性问题时，它们的优势更为显著。Runge-Kutta方法的核心理念是通过一系列初始试探步骤来逼近实际的函数值，从而减小单步的局部截断误差，进而提高整体的计算精度。 在解决形如 \( y' = f(t, y) \)，已知初始条件 \( y(t_0) = y_0 \) 的微分方程时，Runge-Kutta方法采用迭代的方式进行求解。其基本过程包括以下几个关键步骤： 1. **概念解释**：每个时间步的推进并非直接基于当前状态，而是先通过几个试探步骤（也称为内插步骤），这些步骤模拟了函数 \( f(t, y) \) 在当前和新点之间的行为。这样做的目的是减少每一步的误差贡献。 2. **步骤细化**：对于四阶Runge-Kutta方法，例如，它可能涉及到四个不同的测试步骤，每个步骤根据前一步的结果计算出增量，然后将这些增量组合以得到最终的新状态。 3. **方法的阶数**：Runge-Kutta方法的阶数决定了其全局准确度。一个二阶方法，比如使用步长 \( h \) 进行计算，理论上，误差随时间的增加会以 \( O(h^2) \) 的速度减小。这意味着随着步长的减小，方法的精确度将显著提升。 4. **优势与应用**：这种高阶性质使得Runge-Kutta方法特别适合于需要长期高精度模拟的科学和工程计算，尤其是在涉及敏感性依赖或者系统稳定性分析的情况下，这些方法能够提供可靠的结果。 总结来说，《odes_runge_kutta.pdf》主要介绍了Runge-Kutta方法的原理、优点以及在解决常微分方程中的应用，强调了通过多步内插和更高阶的准确性来提高数值解的稳定性和精确度。这对于理解数值计算中复杂问题的近似求解策略具有重要意义。