"基于圆锥曲线和直线融合特征的长焦相机高精度标定方法研究"

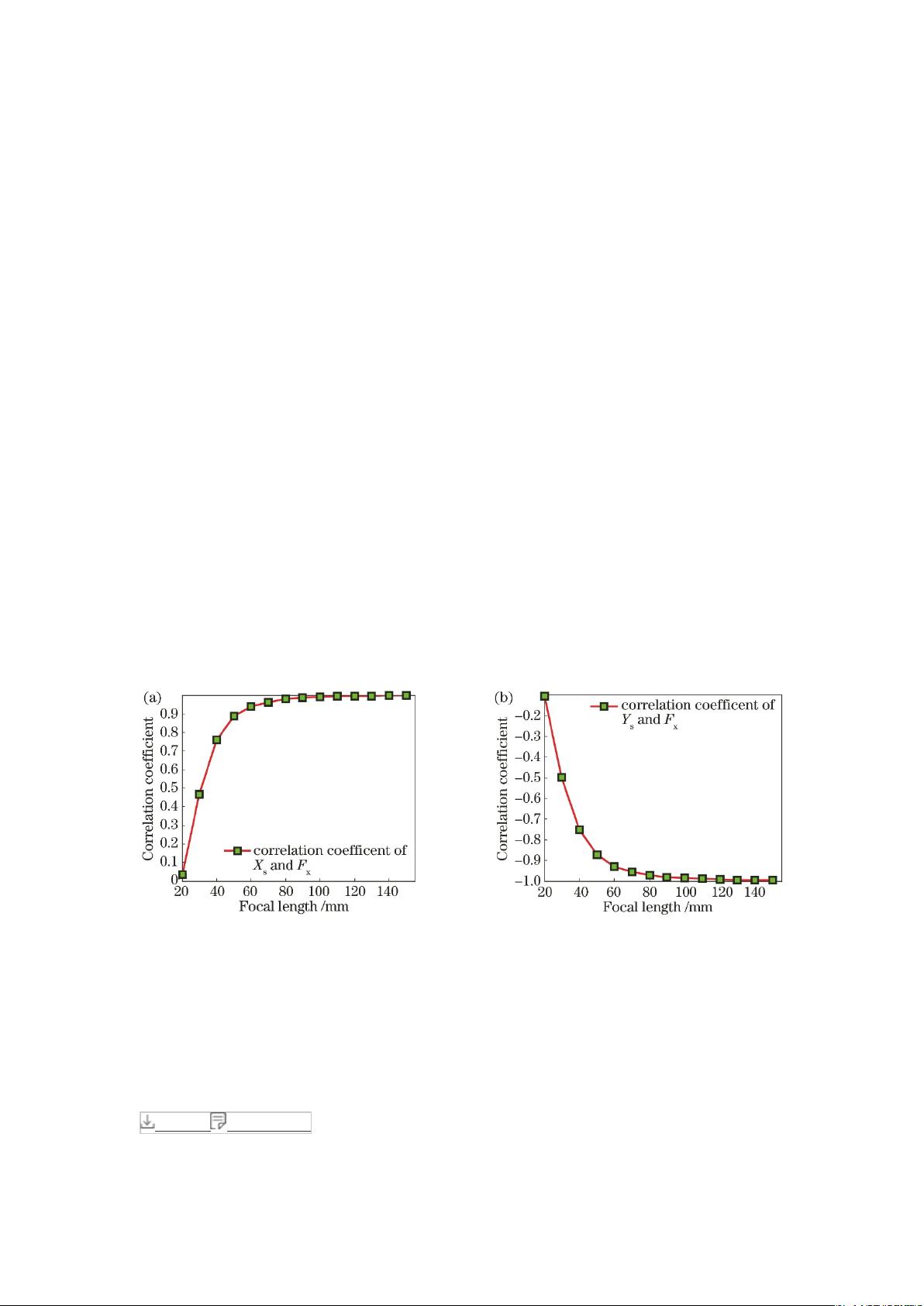
Abstracting at the bottleneck of telephoto camera calibration, a novel calibration method based on conics and line fusion features is proposed in this study. The article explores the formation mechanism of ill-conditioned calibration equations of telephoto cameras and designs a concentric half-circle planar template based on the unique properties of perspective transformation, such as invariant cross ratios and invariant tangents. By combining the normalized line homography estimation method and partial regularity estimation theory, the high-precision and robust initial values of the internal and external parameters of telephoto cameras are solved. Taking into account the influence of lens distortion, the method introduces the line segment integral distance measure and uses the minimization of the distance from the model line to the projection plane as the objective function. Nonlinear iterative optimization algorithms are then employed to solve the calibration parameters. Simulation and experimental results demonstrate the correctness and effectiveness of the proposed telephoto camera calibration method. Furthermore, compared to traditional calibration methods, the proposed method exhibits superior calibration accuracy and robustness. In conclusion, the proposed calibration method based on conics and line fusion features effectively addresses the existing challenges in telephoto camera calibration. By leveraging the unique properties of conic curves and lines in perspective transformation, the method achieves high precision and robust solutions for the internal and external parameters of telephoto cameras. The introduction of the line segment integral distance measure further enhances the calibration accuracy, making the proposed method more effective and reliable. Overall, the study contributes significantly to the advancement of telephoto camera calibration technology and provides a solid foundation for future research in this field.