JCAP11(2016)025
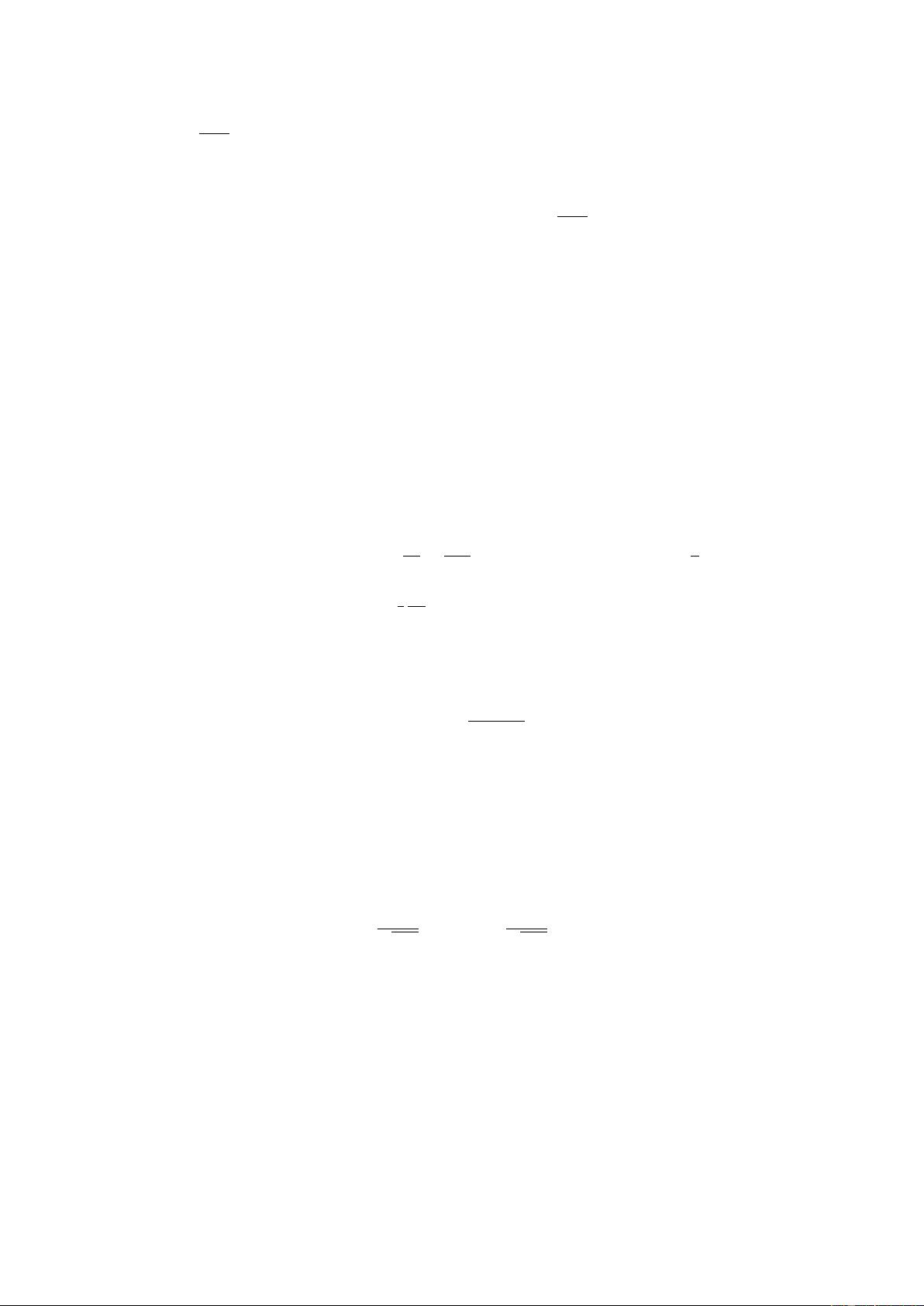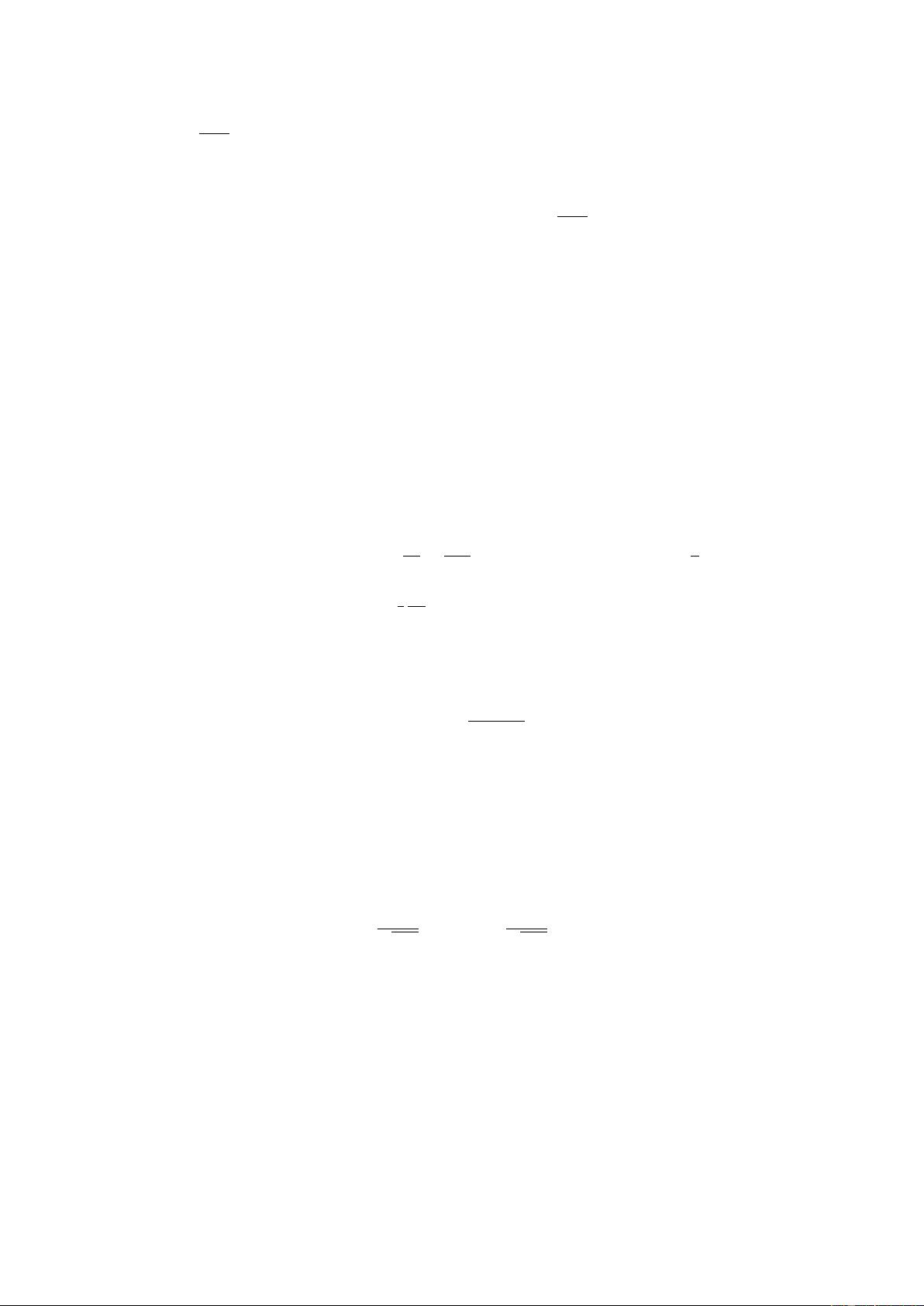
where
p
hh
2
i plays the role of the relevant energy scale at which the coupling should be
evaluated. Since we are only interested in the high energy regime, in our numerical analysis
we use the step-function approximation
λ
h
(µ) = 0.01 × sign
h
SM
c
−
p
hh
2
i
, (2.8)
where h
SM
c
∼ 10
10
GeV is the critical scale of the Standard Model at which λ
h
flips sign.
3 Pure parametric resonance
Let us first consider the case where the trilinear interaction is negligible, σ
hφ
≈ 0. The
Higgs-inflaton interaction is quartic so that we recover the well-known parametric resonance
setting [16].
The equations of motion for the Higgs field are quadratic in h apart from the quartic
self-interaction. During the parametric resonance regime, the effect of the latter can be
approximated as h
4
→ 6h
2
hh
2
i, which is known as the Hartree approximation. In that case,
the equations of motion for different momentum modes decouple. In terms of the rescaled
Higgs momentum modes X
k
≡ a
3/2
h
k
, where a is the scale factor, one has [16]
¨
X
k
+ ω
2
k
X
k
= 0 with ω
2
k
=
k
2
a
2
+
λ
hφ
2
Φ
2
cos
2
(mt) + 3λ
h
a
−3
hX
2
i +
3
2
wH
2
. (3.1)
In the last term, w = p/ρ = −
1 +
2
3
˙
H
H
2
is the equation of state parameter of the Universe,
which vanishes in the matter-like background. We thus neglect this term.
If the Higgs-inflaton coupling λ
hφ
is substantial, the Higgs modes experience amplifica-
tion due to broad parametric resonance. The parameter characterizing the strength of the
resonance is
q(t) =
λ
h
Φ
2
(t)
2m
2
(3.2)
such that q 1 corresponds to the broad resonance regime. In this case, the modes grow
exponentially leading to a large Higgs field variance hh
2
i. The fluctuations can be so signif-
icant that they exceed the size of the barrier separating the electroweak vacuum from the
catastrophic one at large field values. In this case, vacuum destabilization occurs. In what
follows, we will estimate the corresponding critical size of λ
hφ
.
As was shown in [16], in the broad resonance regime the Higgs modes evolve adiabatically
away from the inflaton zero-crossings and can be described by the WKB approximation
X
k
'
α
k
√
2ω
k
e
−i
R
ω
k
dt
+
β
k
√
2ω
k
e
i
R
ω
k
dt
, (3.3)
where α
k
, β
k
are some constants. Adiabaticity is broken for certain modes near the inflaton
zero-crossing, where the frequency ω
k
evolves very quickly. There the system can be treated
in analogy to the Schr¨odinger equation as a scattering of plane wave solutions. The adiabatic
constants α
k
and β
k
can be thought of as Bogolyubov coefficients. We assume a vacuum
initial condition for the Higgs modes with α
k
= 1 and β
k
= 0. The occupation number of
Higgs quanta after j ' mt/π zero crossings is then
n
j+1
k
= |β
j+1
k
|
2
(3.4)
– 4 –
剩余22页未读，继续阅读
weixin_38713306
- 粉丝: 3
- 资源: 883
我的内容管理
展开
最新资源
- Hadoop生态系统与MapReduce详解
- MDS系列三相整流桥模块技术规格与特性
- MFC编程：指针与句柄获取全面解析
- LM06：多模4G高速数据模块，支持GSM至TD-LTE
- 使用Gradle与Nexus构建私有仓库
- JAVA编程规范指南：命名规则与文件样式
- EMC VNX5500 存储系统日常维护指南
- 大数据驱动的互联网用户体验深度管理策略
- 改进型Booth算法：32位浮点阵列乘法器的高速设计与算法比较
- H3CNE网络认证重点知识整理
- Linux环境下MongoDB的详细安装教程
- 压缩文法的等价变换与多余规则删除
- BRMS入门指南：JBOSS安装与基础操作详解
- Win7环境下Android开发环境配置全攻略
- SHT10 C语言程序与LCD1602显示实例及精度校准
- 反垃圾邮件技术：现状与前景
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
