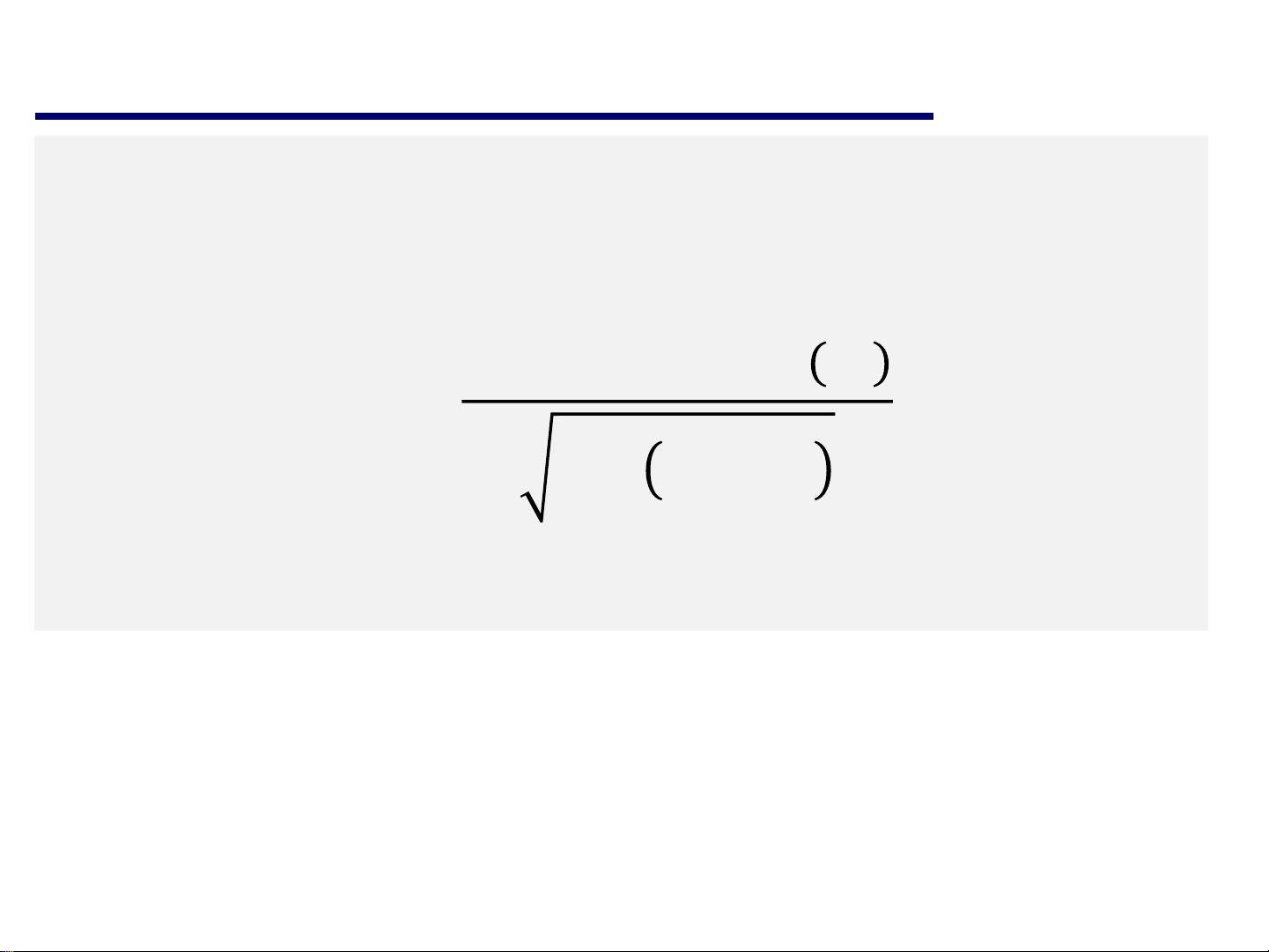林德贝格-勒维中心极限定理与大数定律解析

"第二十四次课PPT1 - 矩阵、中心极限定理与大数定律" 在第二十四次课中，主要讨论了几个重要的概率论和统计学概念，特别是与矩阵、中心极限定理相关的知识。首先，回顾了随机投影的概念，这涉及到将高维数据通过随机矩阵进行降维的过程。在随机投影中，定义了一个函数𝑓𝑓(𝑥𝑥)，它使用随机矩阵𝑃𝑃(𝑑𝑑×𝑘𝑘)，其中每个元素独立且服从标准正态分布𝑁𝑁(0,1)，将原始数据𝑥𝑥变换为较低维度的𝑦𝑦𝑖𝑖。JL-引理阐述了在满足一定条件时，随机投影能够保持高维空间中点之间的距离，这对于数据压缩和近似计算具有重要意义。 接着，课程回顾了几种不同类型的大数定律，这是概率论中的基础定理，描述了随机变量序列的平均行为趋于稳定的情况。Markov大数定律指出，如果随机变量序列的方差之和随样本数量𝑛𝑛增加而减少，那么该序列的平均值将趋向于一个确定值。Chebyshev大数定律则是在随机变量的方差有界时，确保了平均值的稳定性。Khintchine大数定律适用于独立同分布的随机变量，而Bernoulli大数定律特指二项分布的随机变量，其样本均值将趋向于概率𝑝𝑝。 然后，课程的重点转向了中心极限定理，这是一个在概率论中极其重要的定理，它描述了独立同分布的随机变量序列的标准化和求和结果，随着样本数量的增加，其分布会接近正态分布。林德贝格-勒维(Lindeberg-Lévy)中心极限定理是中心极限定理的一个具体形式，它规定了在期望值为𝜇𝜇，方差为𝜎𝜎^2的独立同分布随机变量下，标准化和求和的随机变量YN趋于标准正态分布Nd(0,1)。这意味着，即使原始随机变量的分布不是正态的，它们的平均值也将趋向于正态分布，这是许多统计推断和假设检验的基础。 最后，课程提到了标准正态分布的分布函数Φ𝑥𝑥，并指出林德贝格-勒维中心极限定理的另一种表述方式，即随机变量YN的分布函数在𝑛𝑛趋向无穷时，趋近于标准正态分布的分布函数。 这些理论在实际应用中有着广泛的应用，例如在机器学习中的降维技术、数据预处理、假设检验以及统计推断等领域。理解并掌握这些概念对于深入学习和应用统计学和概率论至关重要。