华南师大讲稿：ACM程序设计中的优先队列与左偏树详解

在ACM程序设计中，堆和左偏树是重要的数据结构和算法工具，尤其在优先队列的应用中发挥着核心作用。堆，特别是二叉堆（最小堆和最大堆），是一种特殊的完全二叉树，其中每个节点的值要么大于或等于其子节点，要么小于或等于其子节点，这确保了堆的性质，使得查找、插入和删除操作具有高效性。最小优先队列和最大优先队列是堆的主要应用场景，它们分别用于寻找优先级最小或最大的元素。 在 ACM 竞赛中，优先队列被广泛应用于各种问题，包括统计问题、最值问题、模拟问题和贪心策略。二叉堆由于其简单的实现和高效性，常被用于解决这类问题。然而，当需要同时处理两个或更多优先队列时，二叉堆的性能不再理想，这就引出了左偏树的概念。 左偏树是一种改进的堆结构，它允许更高效地合并多个优先队列。通过将每个节点与其所有右子节点关联起来，形成一种类似于链表的结构，左偏树能够在合并过程中保持较低的时间复杂度，特别是在插入和删除操作上。这种设计思想源于二分查找和树形结构优化，旨在进一步减少操作时间。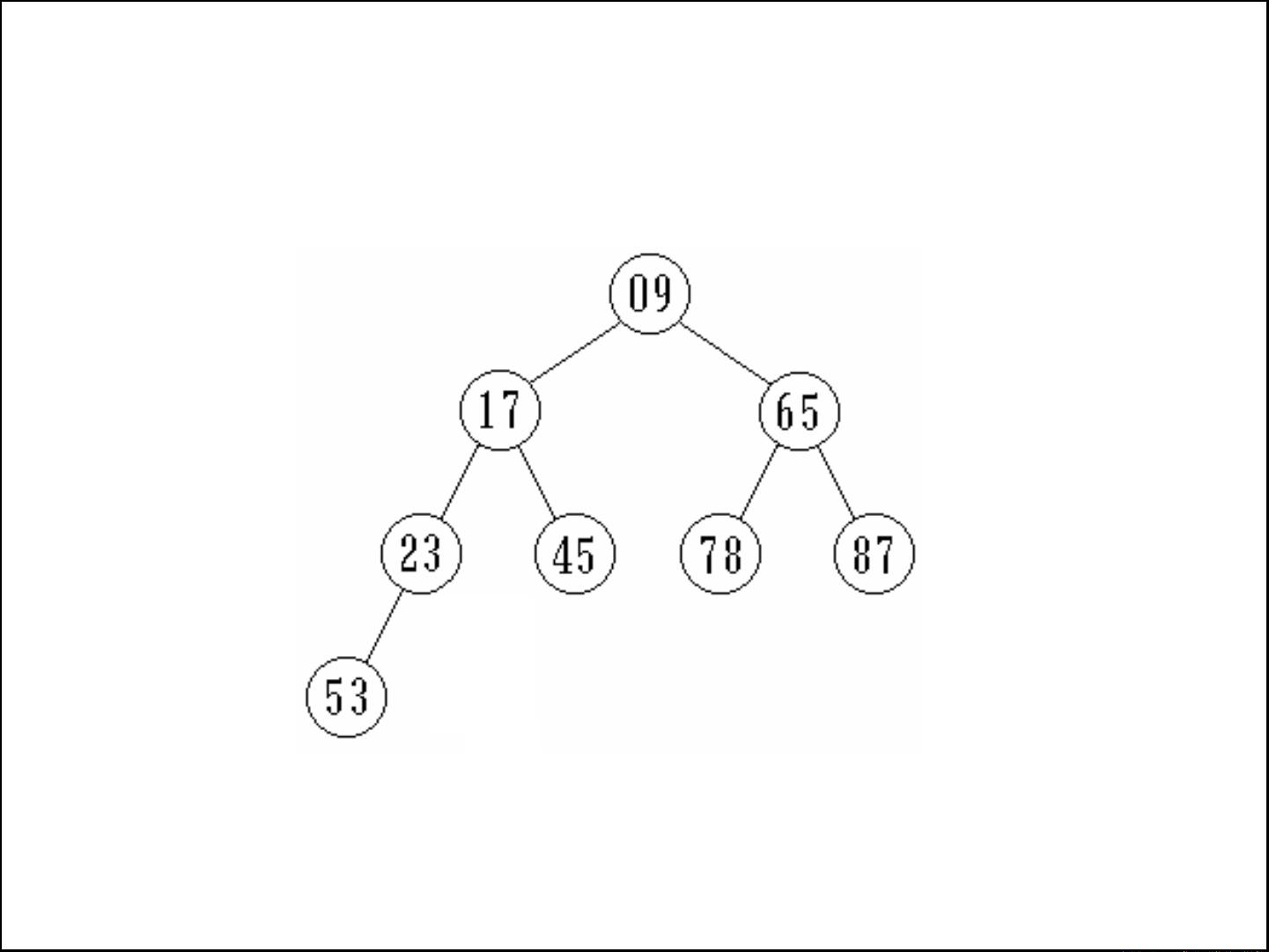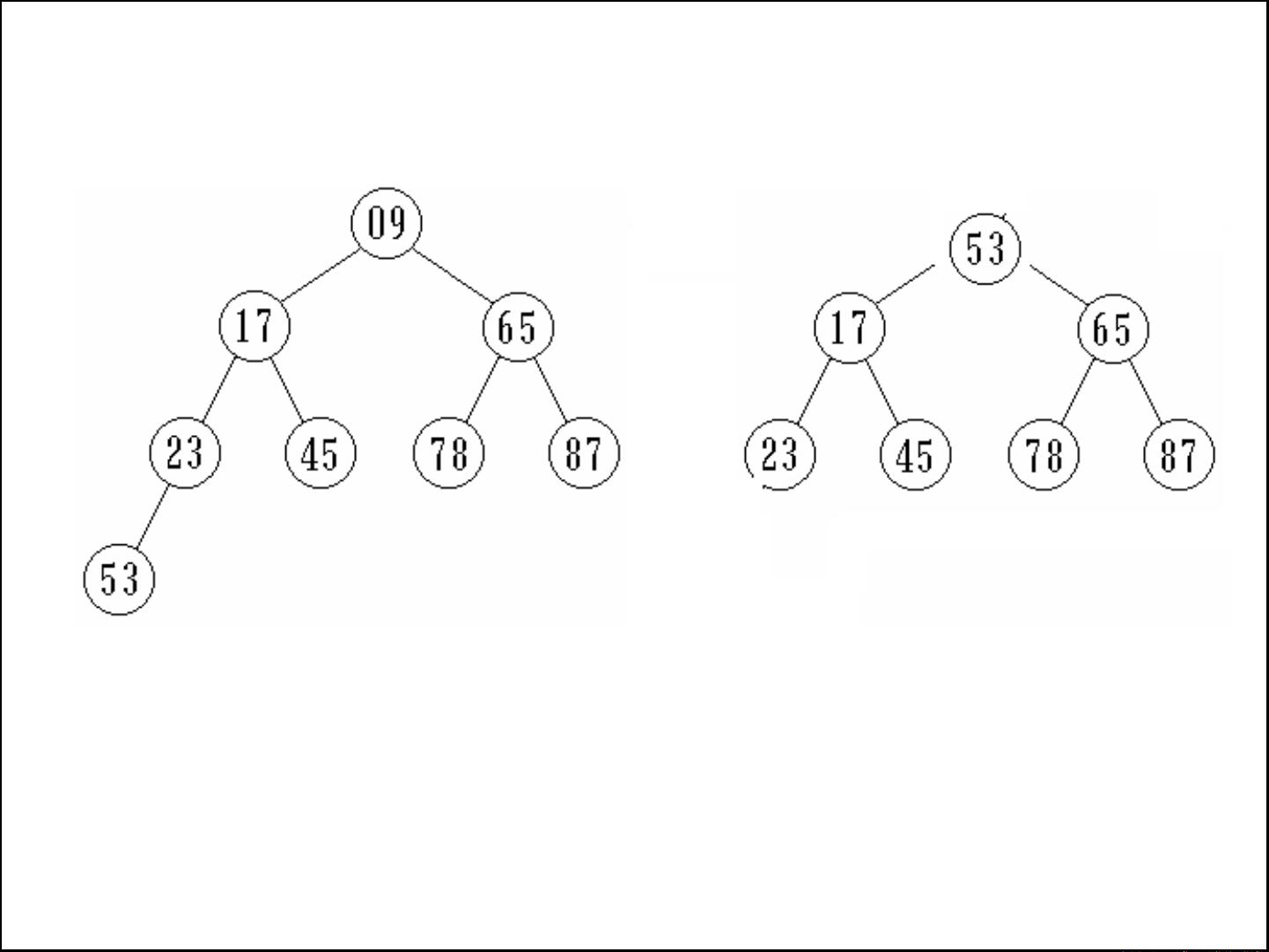 堆操作包括插入和删除，例如在最大堆中，插入元素时总是将其放在适当的位置以维护堆的性质，而删除操作通常涉及调整堆以保持最大（或最小）堆的特性。对于最小堆，插入11和删除操作也是类似的，但遵循相反的比较规则。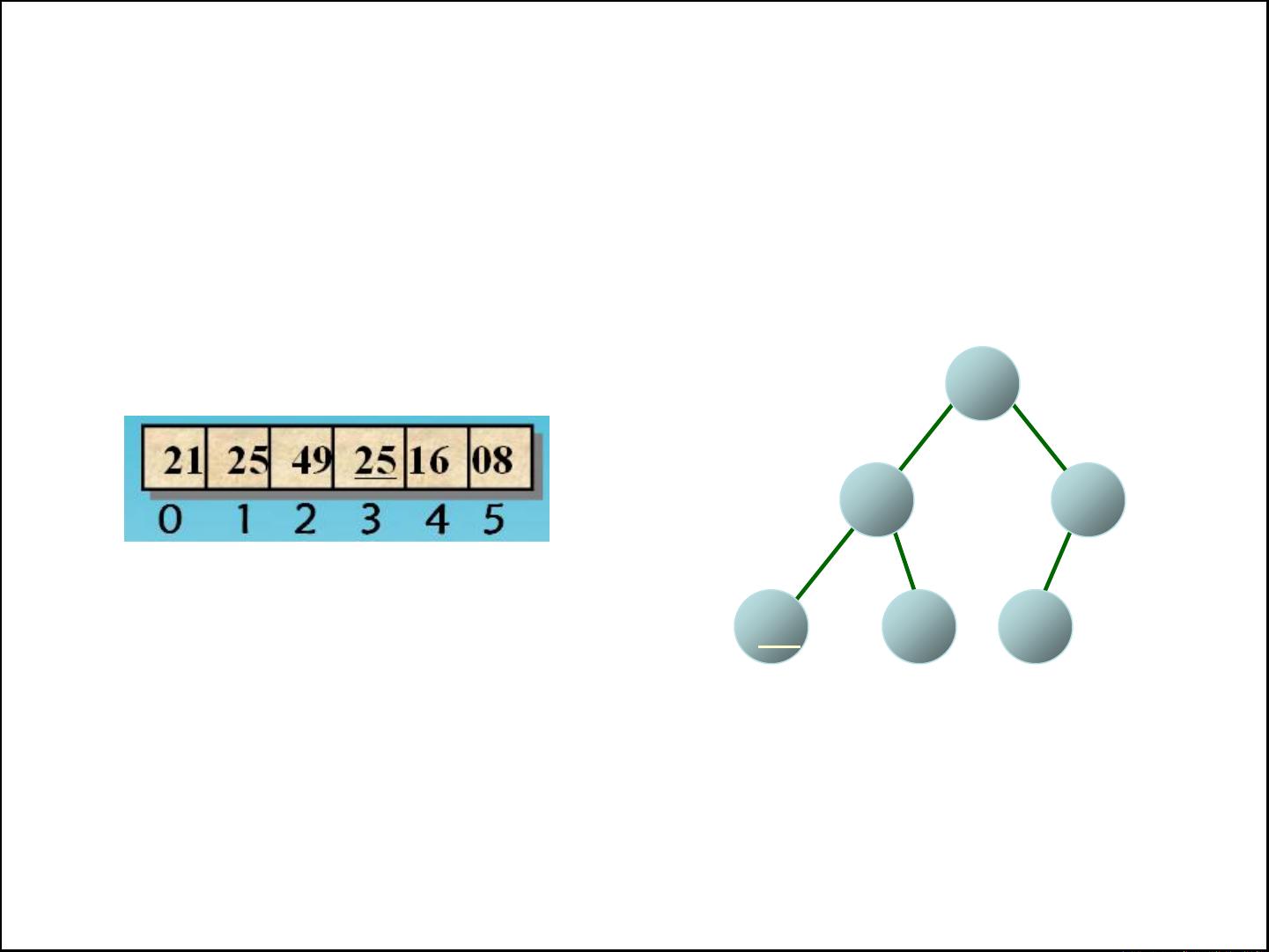 堆的存储结构利用了完全二叉树的特性，通过顺序存储在数组中实现，比如用一维数组动态地表示堆中的节点。这样，节点间的逻辑关系可以通过数组下标直接访问，方便进行高效的插入和删除操作。数组存储时，对于给定的元素序列，如21, 25, 49, 25, 16, 08，可以通过计算每个元素的正确位置来构建堆。 堆和左偏树在ACM程序设计中是不可或缺的，不仅因为它们提供了高效的优先队列解决方案，还因为它们是解决复杂算法问题的关键数据结构，对于理解算法设计和竞赛解题技巧至关重要。掌握这些概念和技术，将有助于提升编程能力，并在实际编程挑战中取得成功。