机器学习入门：一步步解析SVM算法

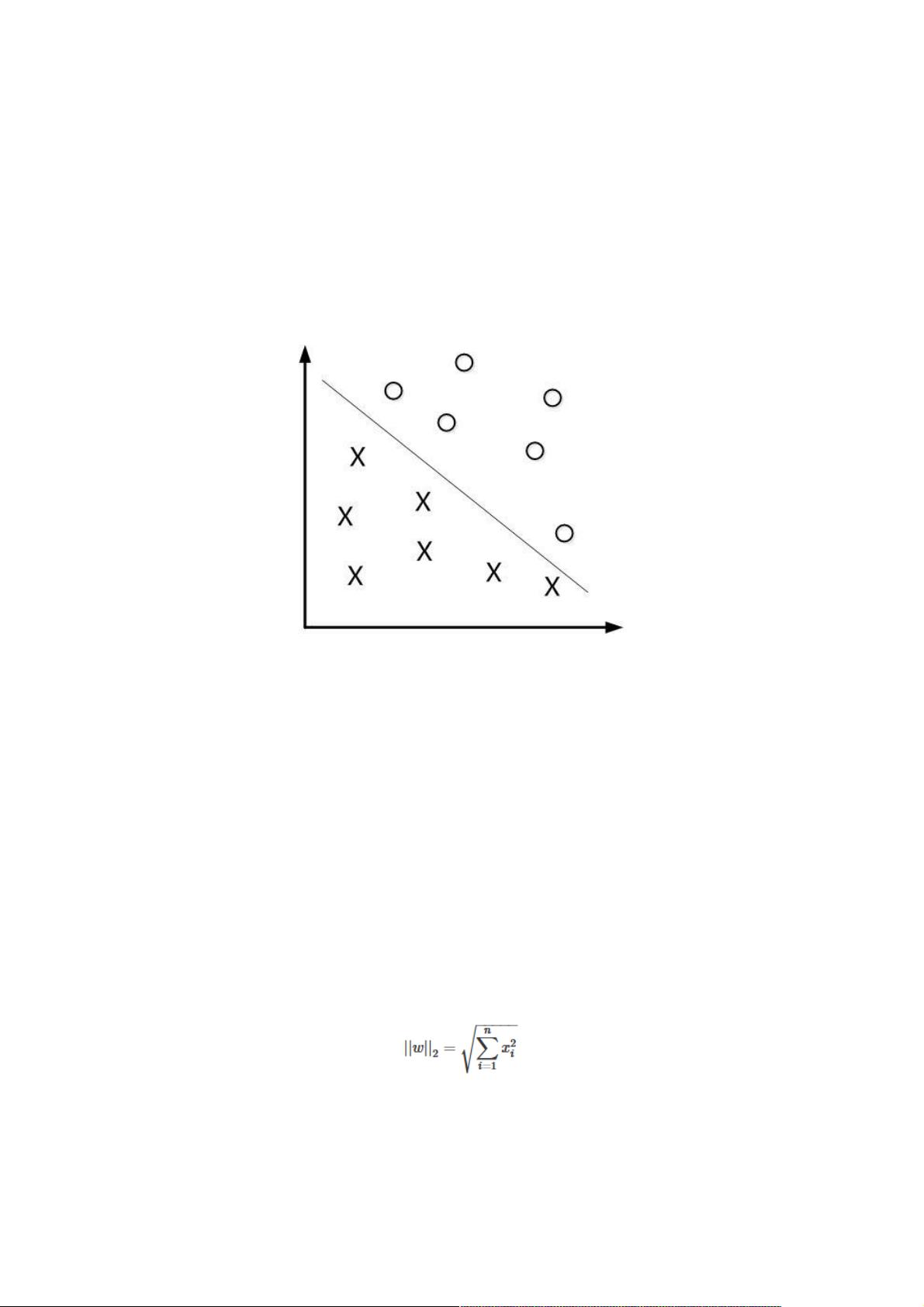
"这篇文章除了介绍SVM的基础概念，还从实践角度展示了如何用SVM进行图像分类，特别是猫狗分类的例子。作者强调，SVM是一种有效的二分类模型，旨在找到一个最佳的超平面将不同类别的数据点分离。文章通过CIFAR数据集的实例，解释了训练与预测的流程，并探讨了SVM的核心思想——最大化间隔。" 在机器学习领域，支持向量机（SVM）是一种广泛使用的监督学习模型，尤其适用于分类问题。SVM的核心目标是寻找一个能够将不同类别数据点最大程度分开的决策边界，也就是所谓的超平面。这个超平面是由权重向量w和偏置项b定义的直线或高维超平面，其方程为wTx + b = 0。 在实际应用中，比如猫狗图像分类，我们需要先获取训练数据集，如CIFAR数据集中提取出猫和狗两类样本。接着，构建训练样本集D，其中每个样本由特征向量x和对应的类别标签y组成。在SVM中，标签y通常取+1或-1，分别代表两个不同的类别。 为了找到最优超平面，SVM引入了最大间隔的概念。间隔是指样本点到超平面的距离，计算公式为r = |wTx + b| / ||w||，其中||w||表示w的L2范式，即向量w的欧几里得长度。SVM的目标是找到一个超平面，使得各类别样本到它的距离最大，这样可以提高模型对新样本的泛化能力，因为它能更好地应对数据的噪声和小的偏差。 在实践中，我们通常利用优化算法（如拉格朗日乘子法）来解决这个问题，寻找满足间隔最大化的w和b。优化过程会涉及构造拉格朗日函数，其中包含惩罚项以确保样本点不会落在错误的一侧。这里的1常量在拉格朗日乘子中是为了简化计算，但其实可以是任意非零值，选择1主要是因为方便和直观。 SVM还有其他重要的概念，例如软间隔和核技巧。软间隔允许一部分样本点落在超平面的错误一侧，通过惩罚这些违反间隔的点来平衡分类准确性和模型复杂度。而核技巧则能将数据映射到高维空间，使得原本线性不可分的数据在新的空间中变得线性可分，比如使用著名的径向基函数（RBF）核。 总结来说，SVM是一种强大的二分类工具，通过找到最优超平面实现样本的高效分类。从零开始学习SVM，不仅需要理解其基本原理，还要掌握如何运用到实际问题中，如数据预处理、模型训练、参数调优等。通过不断实践和理论学习，可以逐渐掌握这个复杂的机器学习算法。