C语言实现最大流算法：原理与程序解析

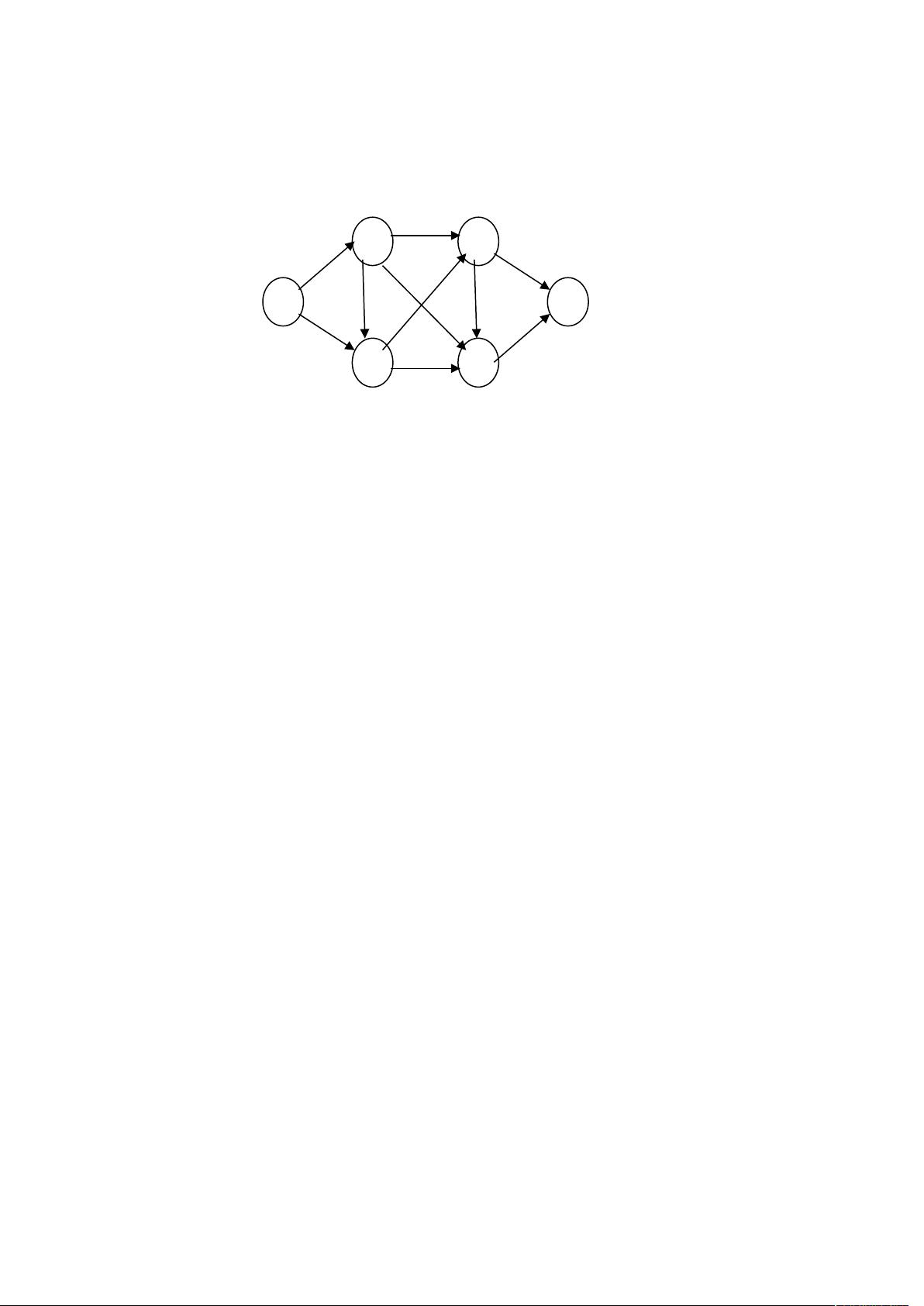
"最大网络流"是图论中的一个重要概念，用于解决在网络中分配流量的问题，使得流量从源节点到汇节点的最大化，同时满足每条边上的流量不超过其容量限制。这个题目展示了如何使用C语言实现一个基本的 Ford-Fulkerson 算法来求解这个问题。算法的核心步骤包括初始化网络结构、标号过程、寻找增广路径以及更新流。 首先，程序定义了三个矩阵：关系矩阵GraphMatrix、容量矩阵cStreamMatrix和初始流量矩阵fStreamMatrix。关系矩阵表示网络中节点之间的连接，容量矩阵则定义了每条边的最大传输能力，而初始流量矩阵初始化为零，表示没有流量通过。 结构体NetNodeType用来存储每个节点的信息，包括一个标志（表示边的状态，可能是通路或未通路）、容量（cStream）和已通过的流量（fStream）。另一个结构体NodeType表示节点，包含节点的标识（Label）和当前流值（Stream）。 函数Initialize()用于初始化这些变量，设置每个节点的标志、容量和初始流量为0，同时设置源节点的流值为最大流上限。 函数Find_Maximum_Stream()则是主要的求解部分： 1. 定义变量dStream为最大流的上限，通常设为一个足够大的常数。 2. 标号过程（BFS或DFS）从源节点开始，为其分配一个唯一的标识，并将流值设为最大流上限。然后逐个遍历其他节点，检查是否有未被占用的通路。 3. 在循环中，寻找一条增广路径，即一条可以增加流量且不会超过容量限制的路径。这可以通过使用深度优先搜索（DFS）或广度优先搜索（BFS）在已经标号的节点中查找。 4. 如果找到增广路径，就更新每条边的流量，使流量沿着这条路径从源节点流向汇节点。更新过程中，会检查路径上的每条边，确保流量不超过其容量。 5. 当无法找到增广路径时，说明已经找到了当前的最大流，此时dStream就是最大流的实际值。 这个C语言程序展示了如何应用最简单的最大流算法求解问题，虽然它可能不适用于大规模网络，但对于教学和理解基本原理非常有用。在实际应用中，更高效的算法如Edmonds-Karp、Dinic's algorithm或Floyd-Warshall可能会处理更大规模的网络。 总结来说，最大网络流是图论中的基础概念，通过C语言程序，我们可以学习如何利用Ford-Fulkerson方法寻找网络中可能的最大流量。理解这个算法有助于我们在实际工程中设计网络流量优化策略。