优化固态硬盘读写性能：树索引设计与实验验证
需积分: 9 121 浏览量
更新于2024-07-09
收藏 3.19MB PDF 举报
本文探讨了固态驱动器（SSD）上的读/写优化树索引设计问题，随着现代SSD技术的发展，传统的索引策略已不能充分利用其优势。固态存储的一大特性是不对称的读写延迟，即读取速度快于写入，而闪存的频繁不规则更新也对其性能产生了影响。过去的优化主要侧重于减少随机写入，但这往往伴随着大量的额外读取，牺牲了部分效率。
为解决这一问题，研究人员提出了一个针对SSD的新型树索引结构。该索引通过引入更新缓冲区和溢出页来减少随机写入次数，降低了数据更新对性能的影响。同时，Bloom过滤器被用来减少在处理索引中溢出节点时的额外读取，进一步提高了读取效率。这样，设计的目标是降低写入和额外读取的成本，从而提升整体的SSD感知性能。
Bloom过滤器的参数选择至关重要，通过调整其假阳性率，可以在保持索引性能的同时平衡读写操作。作者强调，他们的实验结果显示了这种优化方案的有效性，并认为这相较于现有的闪存感知索引是一种进步。论文的研究成果发表在《VLDB Journal》上，对于数据库系统设计者和固态存储优化者来说，这篇论文提供了重要的理论基础和实践指导，有助于改进SSD的索引管理，提升存储系统的响应速度和利用率。
Read/write-optimized tree indexing for solid-state drives
Fig. 4 Element mapping in a Bloom filter
hash functions h
1
(x), h
2
(x),…,h
k
(x). Second, we set all
bits BF[h
i
(x)]to1.
For answering the membership query like y ∈ S,wefirst
calculate the k values of hash functions h
1
(y), h
2
(y),…,
h
k
(y). Then, we check all the Bloom filters of each element
in S and see whether all the BF[h
i
(y)] are 1. If not, y is
not a member of S. If all the BF[h
i
(y)]are1,y may be
in S. Due to the possibility of collisions among the hash
functions, there is a nonzero false-positive probability when
evaluating membership queries on Bloom filters. Given n, k,
and m, previous results [7] have shown that the false-positive
probability of a Bloom filter can be computed by Eq. (3.1).
Further, it is demonstrated that the false-positive probability
is minimalized when k = 0.7
m
n
, which is approximately
0.6185
m
n
.
f
BF
= (1 − e
−kn
m
)
k
(3.1)
However, the Bloom filter does not support deletions of ele-
ments. A recent study [7] enhances Bloom filters to support
deletions.
Bloom filters are space efficient. In addition, they are time
efficient for inserting elements and answering membership
queries. Therefore, we incorporate Bloom filters into B+-
tree-based indices for SSDs to improve search performance.
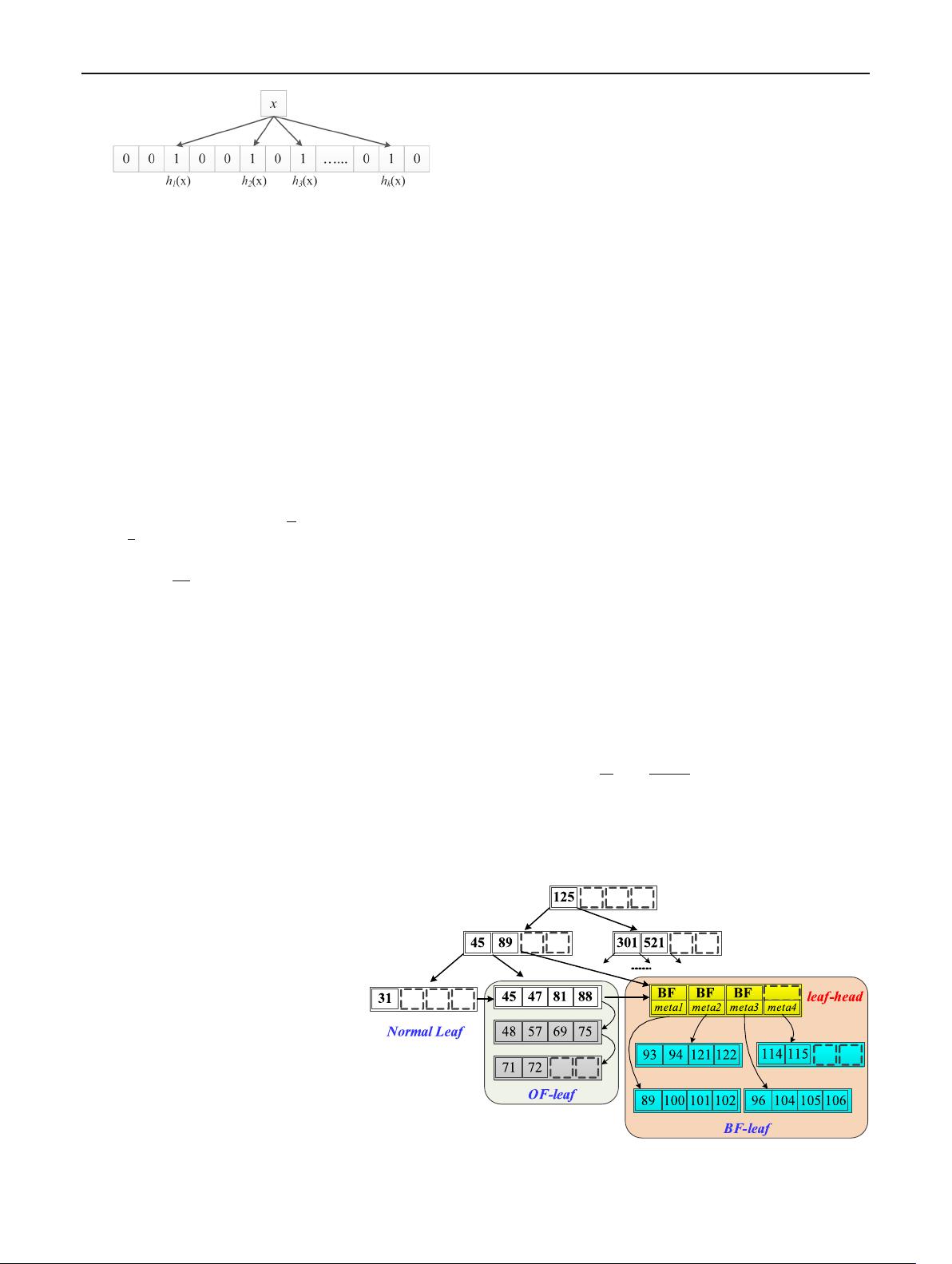
3.3 Structure of the BloomTree
Figure 5 shows the structure of the BloomTree. We improve
the traditional B+-tree with two new designs. First, we
introduce three kinds of leaf nodes, namely Normal Leaf,
Overflow Leaf (OF-leaf ), and Bloom Filter Leaf (BF-leaf ).
Second, we propose to construct Bloom filters in the BF-leaf
nodes and use overflow pages in the OF-leaf nodes.
A normal leaf node is the same as a leaf node on the tradi-
tional B+-tree, and it occupies exactly one page. An OF-leaf
node contains overflow pages. However, an OF-leaf node
contains at most three overflow pages (covered later in this
section), in order to reduce read costs of OF-leaf nodes. If an
OF-leaf node expands beyond three pages, it is transformed
into a BF-leaf node, which offers a more efficient organi-
zation for overflow pages. A BF-leaf node is designed for
organizing leaves with more than three overflow pages. As
shown in Fig. 5, it contains several data pages and a leaf-head
page maintaining the Bloom filters and metadata.
When searching in the BloomTree, the only difference
from the B+-tree is in how leaf nodes are searched. Searching
a normal leaf node is the same as in the B+-tree. Searching
an OF-leaf node needs to scan the entire list of the overflow
pages in the worst case. When searching a BF-leaf node, we
first compute the Bloom filter of the search key, and then we
compare this Bloom filter with the Bloom filters maintained
in the leaf-head page that are computed for the indexed keys
in the BF-leaf node.
The objective of introducing BF-leaf nodes for t he B+-
tree is to improve the poor read performance imposed by the
overflow-page design. As shown in Fig. 3, the overflow B+-
tree introduces additional read operations that hurt the overall
performance of the index. These additional reads are mainly
incurred by the accesses to overflow pages. Given an OF-leaf
with N nodes, where each node has the same probability 1/N
to be accessed, the expected reads are given by E
OF
-cost.
E
OF-cost
=
N
i=1
1
N
=
N + 1
2
(3.2)
Next, we only need two page reads to search a BF-leaf node,
namely one read for t he leaf-head page and another for read-
Fig. 5 Structure of the
BloomTree
123
123
剩余22页未读，继续阅读
2021-05-07 上传
2023-07-27 上传
2023-07-15 上传
2024-08-30 上传
2023-08-22 上传
2023-09-08 上传
2023-06-01 上传
2024-01-14 上传
2023-07-10 上传
weixin_38732277
- 粉丝: 7
- 资源: 880
我的内容管理
展开
最新资源
- WPF渲染层字符绘制原理探究及源代码解析
- 海康精简版监控软件：iVMS4200Lite版发布
- 自动化脚本在lspci-TV的应用介绍
- Chrome 81版本稳定版及匹配的chromedriver下载
- 深入解析Python推荐引擎与自然语言处理
- MATLAB数学建模算法程序包及案例数据
- Springboot人力资源管理系统：设计与功能
- STM32F4系列微控制器开发全面参考指南
- Python实现人脸识别的机器学习流程
- 基于STM32F103C8T6的HLW8032电量采集与解析方案
- Node.js高效MySQL驱动程序：mysqljs/mysql特性和配置
- 基于Python和大数据技术的电影推荐系统设计与实现
- 为ripro主题添加Live2D看板娘的后端资源教程
- 2022版PowerToys Everything插件升级，稳定运行无报错
- Map简易斗地主游戏实现方法介绍
- SJTU ICS Lab6 实验报告解析
