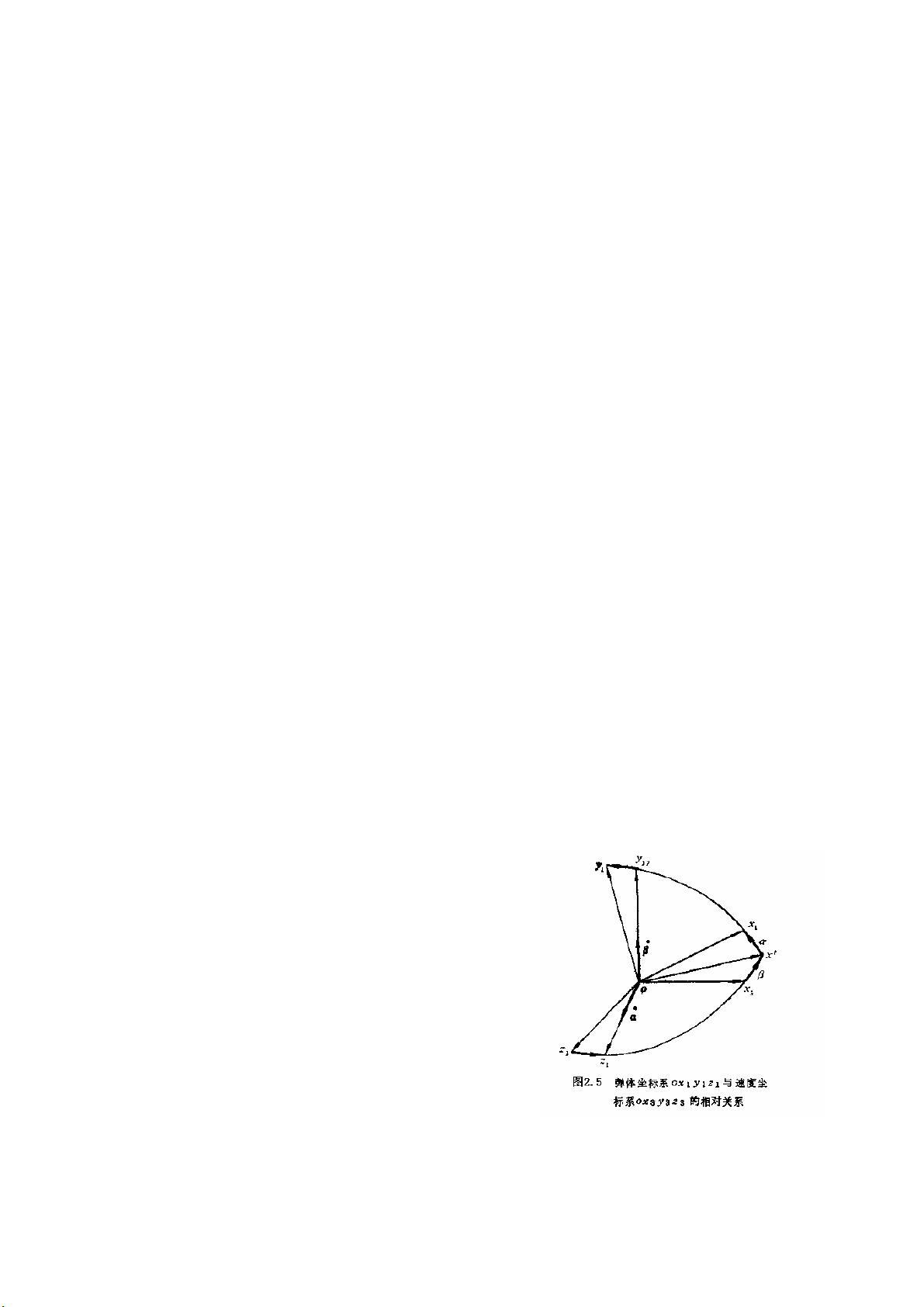
导弹运动方程组的建立与简化方法

本文主要介绍了导弹运动方程组的建立，包括导弹运动的建模基础、简化处理，以及过载概念等相关知识。 导弹运动方程组的建立是研究导弹动力学的关键，它涉及到导弹在空间的运动规律。导弹作为刚体，其运动涉及六个自由度，包括沿三个正交轴的平动和绕这三个轴的转动。在建立导弹运动方程时，通常会选取适当的坐标系，如惯性坐标系和导弹坐标系，以便更准确地描述导弹的运动状态。 1. 坐标系定义和转换：理解坐标系的选择及其引用目的至关重要，例如惯性坐标系用于描述相对于地球的全局运动，而导弹坐标系则便于描述导弹自身的姿态变化。坐标系间的转换涉及到旋转矩阵或四元数，这些工具帮助我们从一个坐标系到另一个坐标系进行描述。 2. 弹道方程组：导弹的运动方程通常包括牛顿第二定律和动量矩定理。对于刚体，牛顿定律用于描述质心的移动，动量矩定理用于研究绕质心的转动。导弹运动方程的完整形式会非常复杂，因为它需要考虑变质量、推力、重力、空气阻力等因素。 3. 简化处理：为了简化分析，导弹的变质量系统经常被假设为常质量，即将导弹与喷射出的燃气质量视为一个整体，应用“固化原理”。同时，忽略一些次要因素，如弹体的弹性变形和非定常流体力学效应。 4. 过载：过载是导弹在飞行过程中经历的加速度，对弹道设计和导弹结构设计有直接影响。过载分为可用过载和需用过载，前者是导弹实际能承受的最大加速度，后者是实现特定机动目标所需的最小加速度。计算和理解过载对于优化导弹性能至关重要。 教学中，通常采用板书推导和多媒体演示相结合的方式，辅以弹道设计的大练习和上机编程实践，以帮助学生深入理解和掌握这些概念。课程内容还包括了如何建立简化导弹运动方程，如平面运动和质心运动方程，并探讨四元数在飞行力学中的应用，这有助于处理导弹姿态控制问题。 通过8个学时的课堂教学，8个学时的上机实践，以及4个学时的大练习，学生可以全面掌握导弹运动方程组的建立方法，理解坐标系转换，熟悉简化处理技巧，以及过载在导弹设计中的作用。这样的学习安排确保了理论与实践的紧密结合，以培养出具备实际解决问题能力的专业人才。