多重插补方法在缺失值处理中的应用

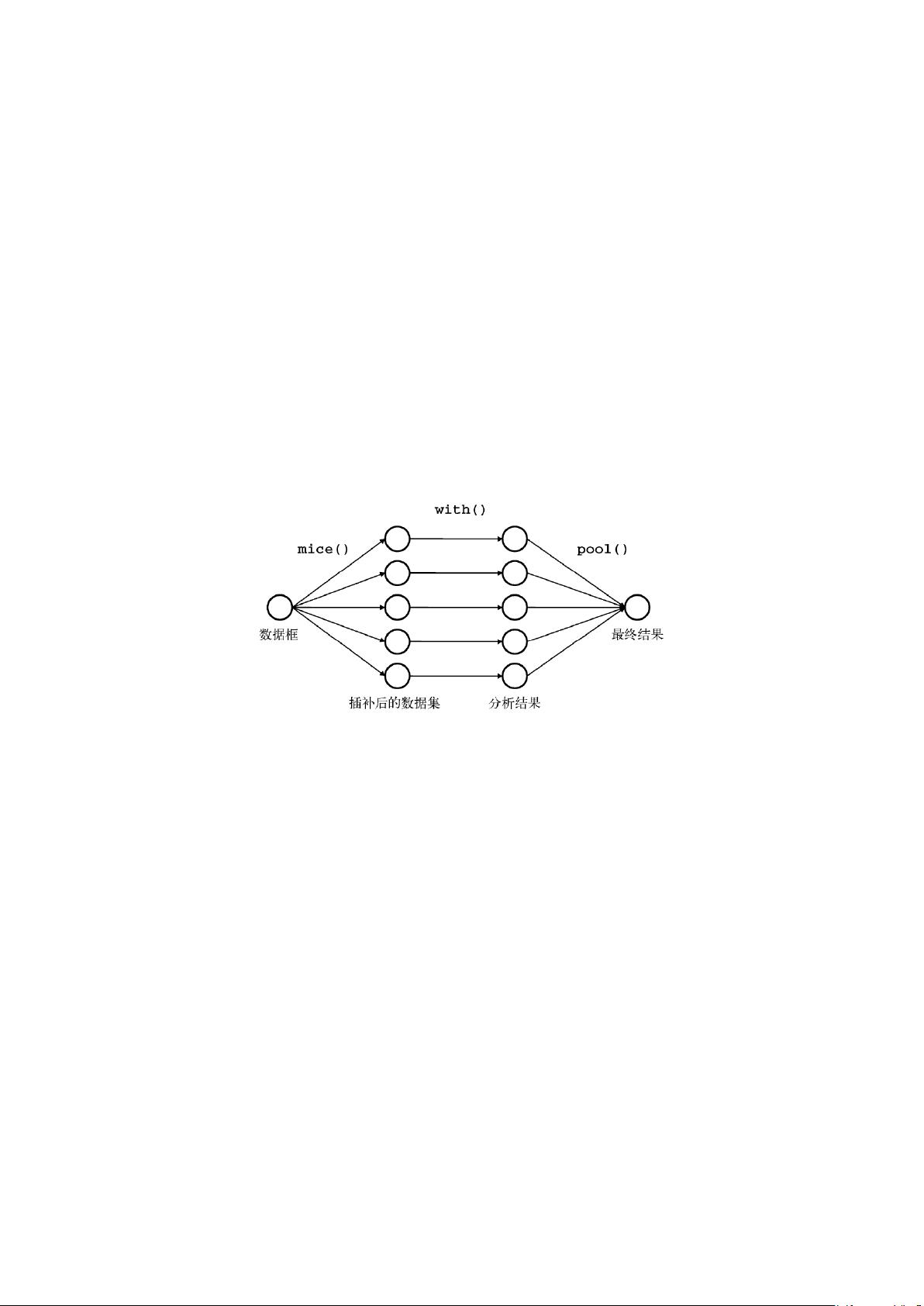
"多重插补方法介绍1" 多重插补（Multiple Imputation，简称MI）是一种处理缺失数据的统计学方法，尤其适用于处理复杂的数据集。这种方法的核心思想是通过生成多组不同的插补数据集来估计缺失值，每组数据集都反映了可能的一种真实情况。在实际操作中，通常会生成3到10组插补数据，以充分捕捉数据的不确定性。 在MI过程中，首先，使用某种插补技术（如均值插补、回归插补、最近邻插补等）来填充数据中的缺失值。在示例中，`method='norm.predict'` 指定了使用具有预测功能的线性回归插值方法。`mice()` 函数在R语言中用于实现这一过程，它接收数据框（如 `data`）以及插补次数（如 `m=5`）作为参数。`mice()` 函数将返回多个完整的数据集，每个数据集都有不同的插补结果，这是因为插补过程中包含了随机成分。 然后，使用 `with()` 函数对每组插补后的数据集执行统计分析，例如，建立线性模型 `lm()` 或广义线性模型 `glm()`。在例子中，`with(imp,lm(qnimeanbp_min~qmeanbp_min))` 是用线性模型分析插补后的数据，其中 `qnimeanbp_min` 和 `qmeanbp_min` 分别代表前12小时的无创收缩压和有创收缩压。这样，我们就可以得到n组统计分析结果，每组结果都基于一个独立的插补数据集。 最后，为了综合这些单独的结果，使用 `pool()` 函数将这n组统计结果合并成一个最终结论。这有助于减少由于缺失值处理引入的偏差，并提供更稳健的统计推断。同时，可以通过 `summary()` 函数查看评估指标，这些指标可以用来评估插补的质量和可靠性。 在实际应用中，选择合适的插补方法和次数（`m` 的值）是非常重要的。如果 `m` 设置得过小，可能会低估缺失值的不确定性；而 `m` 过大则会增加计算负担。在本例中，`m=2` 是为了简化计算，但通常建议使用更大的 `m` 值以获得更好的结果。 总结来说，多重插补方法是一种系统性的处理缺失值的方法，它通过生成多个插补数据集并进行多次统计分析，来提高数据分析的准确性和可靠性。这种方法在处理大规模、复杂数据集时尤为有用，能够有效地应对缺失数据带来的挑战。