小波变换入门：从工程应用视角解析

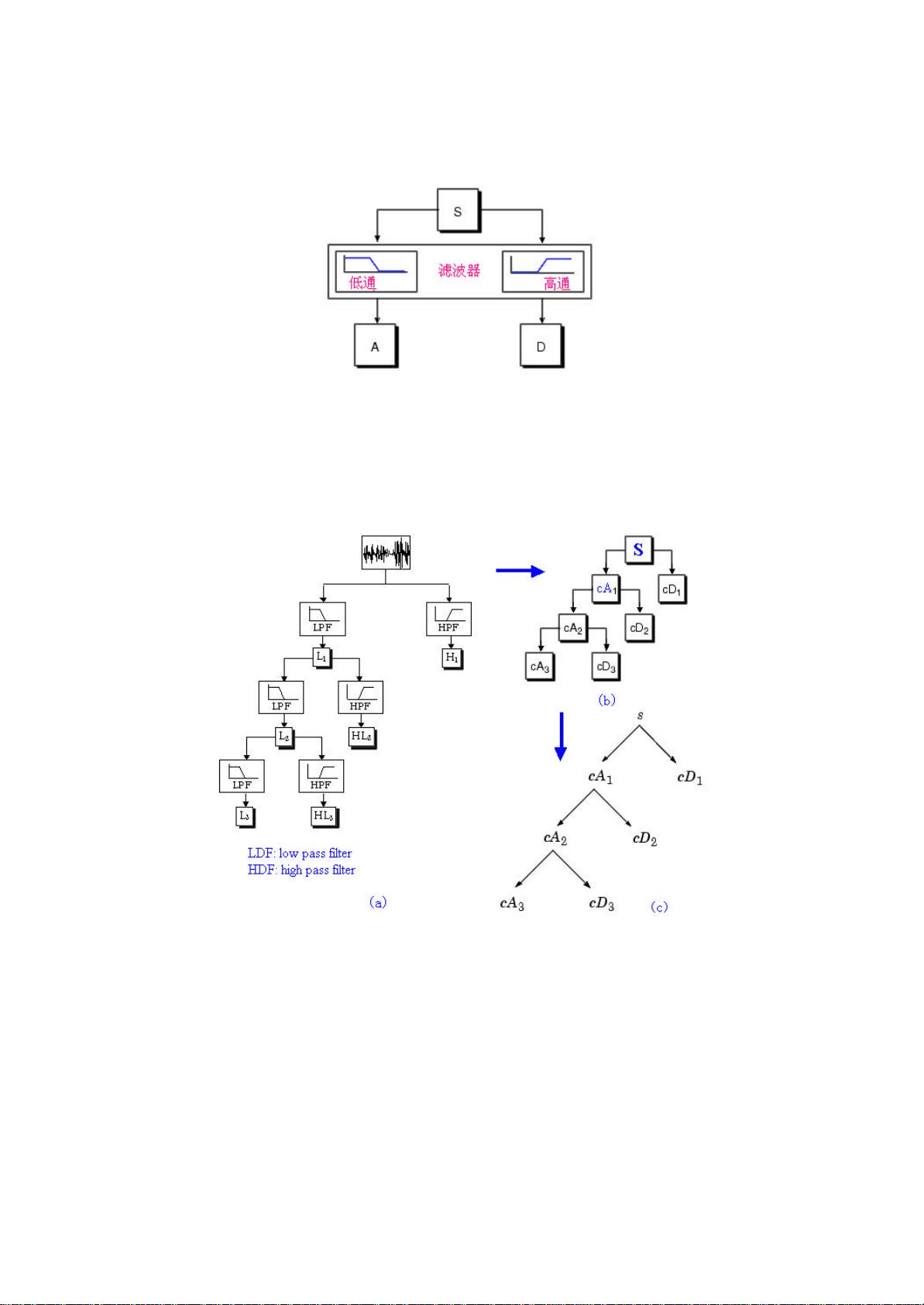
"小波变换和小波分析是数学与工程领域的关键技术，它们在图像处理、语音分析等领域有着广泛的应用。小波分析起源于哈尔在1909年提出的小波概念，经过多位科学家的贡献，如Jean Morlet、Y. Meyer和Stephane Mallat等，逐渐发展成为一种强大的数学工具。Mallat算法是小波变换的重要里程碑，它为正交小波基的构造提供了快速方法。" 小波变换与小波分析是20世纪发展起来的数学理论，它们弥补了傅立叶变换在时间和频率分辨率上的不足。傅立叶变换能够揭示信号的频率成分，但无法精确指示信号发生的时间。小波变换则解决了这个问题，它既能提供频率信息，也能定位信号出现的时刻，因此在信号处理和数据分析中具有显著优势。 小波的历史可以追溯到1909年，当时哈尔提出了第一个小波函数，即哈尔小波。然而，真正推动小波理论发展的是20世纪70年代，Jean Morlet提出的概念以及80年代Y. Meyer的工作。Meyer通过构造具有特定衰减特性的光滑函数，为L(R)空间建立了规范正交基，从而推进了小波分析的理论基础。 Stephane Mallat在1988年的贡献尤为重要，他引入了多分辨率分析的概念，提出了Mallat算法，这是一种构建正交小波基的快速算法。这个算法大大简化了小波变换的计算过程，类似于快速傅立叶变换在傅立叶分析中的作用，使得小波分析得以广泛应用。 小波分析的实用价值在于其灵活性和局部性。不同于傅立叶变换全局分析信号，小波变换允许局部分析，可以捕捉信号的瞬态特征。这在图像压缩、语音识别、故障检测和金融数据分析等多个领域都有重要应用。例如，在图像处理中，小波可以用来提取不同尺度和位置的细节信息；在语音分析中，它可以识别和分离不同频率成分，帮助理解和识别语音信号。 小波变换和小波分析是现代科学和技术中不可或缺的工具，它们结合了频域分析和时域分析的优点，为数据处理提供了更全面、更精细的视角。学习和理解小波理论，对于从事相关领域研究和应用的初学者来说，是提升分析能力的关键步骤。