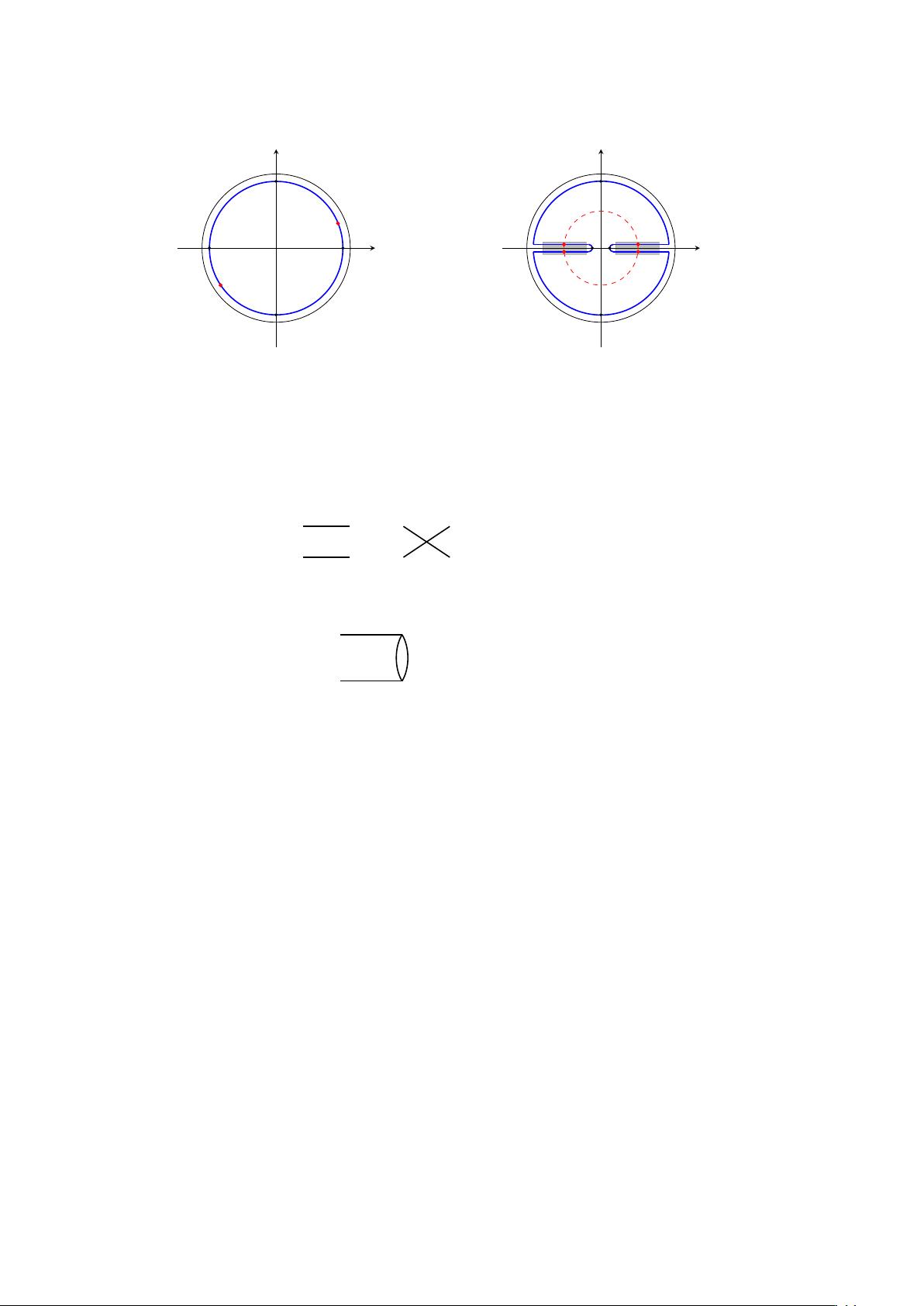
OTOC大小与指数关系：SYK模型和分支时间的探索
133 浏览量
更新于2024-07-16
收藏 435KB PDF 举报
"这篇研究论文探讨了Out-of-Time-Order Correlation (OTOC) 的大小与其指数之间的关系，这是量子混沌理论中的一个重要概念。作者Yingfei Gu和Alexei Kitaev通过深入分析，得出了一个涉及OTOC早期增长指数、指数前因子和所谓的“分支时间”的标识。这个‘分支时间’在动力学平均场框架下被定义，基于延迟核的概念。此标识在 SYK (Sachdev-Ye-Kitaev) 模型及其类似模型中有严格的计算应用，并且在此过程中明确了‘字符串’的定义。
SYK模型是一种特殊的量子系统，常用于研究强关联和量子混沌。在论文中，作者还考虑了一种SYK链的情况。如果耦合强度βJ超过某个临界值，并且忽略那些由OTOCs大小引起的非线性效应，那么蝴蝶效应（即信息传播的速度）所对应的指数将是2π/β。这一结果对理解量子系统的动态行为和混沌性质具有重要意义。
关键词包括：AdS-CFT 对应，1/N 扩展，量子引力模型。这篇论文是在1812.00120号ArXiv上发布的，并且是开放获取的，表明作者保留版权。"
这篇研究工作深化了我们对量子系统混沌行为的理解，特别是在OTOCs如何随着时间演变方面的洞察。OTOCs的增长指数和前因子揭示了系统动力学的关键信息，而“分支时间”则提供了一个新的度量标准，帮助我们更好地理解复杂的量子相互作用。此外，SYK模型和SYK链的研究为探索高维量子引力理论，如AdS-CFT对应提供了有价值的实验平台。通过对这些模型的分析，科学家们可以模拟并研究量子混沌和信息传播的物理过程，这对于未来的量子计算和量子信息科学的发展至关重要。
JHEP02(2019)075
Re e
iθ
Im e
iθ
2
1
3
4
5
6
(a) Time circle
Re e
iθ
Im e
iθ
21
3
4
(b) Deformed (double Keldysh) contour
Figure 2. Integration contours for the Bethe-Salpeter equation (2.9). The deformed contour (b)
is suited for the OTOC calculation, where the main contribution to the integral comes from the
folds shown in gray. There are 4 points (red) on the folds for each value of real time, t = Im θ.
with no rungs:
F
0
(θ
1
, θ
2
, θ
3
, θ
4
) = −
1
2
3
4
+
1
2
3
4
= −G(θ
1
, θ
3
)G(θ
2
, θ
4
) + G(θ
1
, θ
4
)G(θ
2
, θ
3
) .
(2.10)
The integral kernel of the operator K is defined as a product of two-point functions:
K(θ
1
, θ
2
, θ
3
, θ
4
) = −
1
2
3
4
= −J
2
(q − 1)G(θ
13
)G(θ
24
)G(θ
34
)
q−2
. (2.11)
The operator product KF in (2.9) is the integral over two auxiliary points θ
5
, θ
6
on the
time circle, see figure 2 (a):
KF(θ
1
, θ
2
, θ
3
, θ
4
) =
Z
2π
0
dθ
5
Z
2π
0
dθ
6
K(θ
1
, θ
2
, θ
5
, θ
6
)F(θ
5
, θ
6
, θ
3
, θ
4
) . (2.12)
The Bethe-Salpeter equation (2.9) also holds on a deformed contour. The double
Keldysh contour in figure 2 (b) is suited for the calculation of OTOC(t
1
, t
2
, t
3
, t
4
) related
to F by (2.6). We consider this function with t
3
, t
4
fixed and denote it by F (t
1
, t
2
). Since
OTOCs grow exponentially, the KF term is much greater than F
0
, and hence, the latter
may be neglected. Furthermore, the integration contour may be reduced to the union of
two folds, marked as gray area in figure 2 (b), which are then extended to t = −∞. Written
in terms of real times, the equation is reduced to the following form:
Z
folds
dθ
5
dθ
6
K(it
1
+ π, it
2
, θ
5
, θ
6
)F (t
5
, t
6
) ≈ F (t
1
, t
2
) ,
θ
5
= it
5
, it
5
+ π, θ
6
= it
6
, it
6
+ π.
(2.13)
For each value of t
5
, there are four points on the contour, two on the right (with θ
5
= it
5
)
and two on the left (with θ
5
= it
5
+ iπ). The contributions from the first two points cancel
– 4 –
剩余20页未读，继续阅读
2020-03-27 上传
2020-04-18 上传
2020-04-20 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
2024-11-16 上传
2024-11-16 上传
weixin_38667920
- 粉丝: 3
- 资源: 909
我的内容管理
展开
最新资源
- 平尾装配工作平台运输支撑系统设计与应用
- MAX-MIN Ant System：用MATLAB解决旅行商问题
- Flutter状态管理新秀：sealed_flutter_bloc包整合seal_unions
- Pong²开源游戏：双人对战图形化的经典竞技体验
- jQuery spriteAnimator插件：创建精灵动画的利器
- 广播媒体对象传输方法与设备的技术分析
- MATLAB HDF5数据提取工具：深层结构化数据处理
- 适用于arm64的Valgrind交叉编译包发布
- 基于canvas和Java后端的小程序“飞翔的小鸟”完整示例
- 全面升级STM32F7 Discovery LCD BSP驱动程序
- React Router v4 入门教程与示例代码解析
- 下载OpenCV各版本安装包，全面覆盖2.4至4.5
- 手写笔画分割技术的新突破：智能分割方法与装置
- 基于Koplowitz & Bruckstein算法的MATLAB周长估计方法
- Modbus4j-3.0.3版本免费下载指南
- PoqetPresenter：Sharp Zaurus上的开源OpenOffice演示查看器
