浮点数表示法详解：基数、尾数、阶码与IEEE754标准

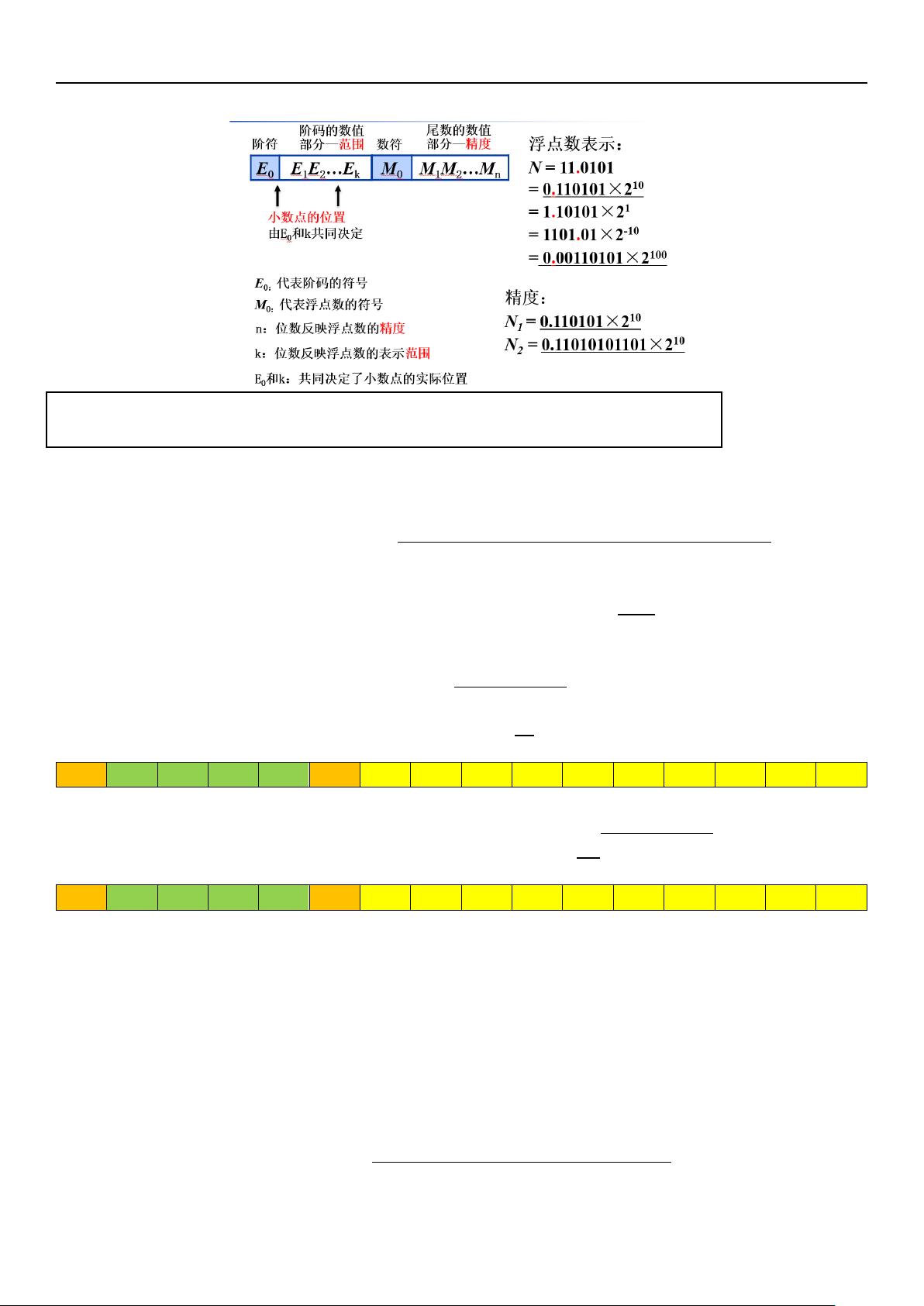
"该资源是一份关于计算机组成原理的第9周课程讲义，主要讨论了定点和浮点数的表示方法，特别是聚焦于IEEE754浮点标准。讲义涵盖了基数、尾数、阶码、精度、范围、规格化等核心概念，并对32位单精度和64位双精度浮点数进行了讲解。" 浮点数表示在计算机科学中扮演着至关重要的角色，因为它们允许我们以有限的存储空间表示大量的数值范围，包括非常大和非常小的数字。在深入理解IEEE754标准之前，我们需要先了解一些基本概念。 **定点表示**是指小数点固定不变的数字表示方式，它通常分为原码、反码和补码三种形式，用于表示整数或有符号的固定小数。然而，定点数在表示大范围数值时存在局限性，如需要较长的位宽，且编程复杂，数据存储效率低。 **浮点表示**则通过将数值分为三个部分来解决这些问题：**基数**（通常是2，但也可以是其他数值）、**尾数**（也称为主数，表示数值的有效数字）和**阶码**（表示数值的大小）。这种表示方法允许动态调整小数点位置，从而可以表示更大范围的数值，同时保持一定的精度。 **精度**指的是浮点数所能表示的小数位数，这直接影响到浮点数的精确度。在IEEE754标准中，精度通常由尾数的位数决定。 **范围**则取决于基数、尾数的位数以及阶码的编码方式。范围包括最小正数（不包括零）和最大负数，以及最大正数。 **规格化**是一种优化浮点表示的方法，确保尾数不以0开头，提高数值表示的效率。这通常通过移动小数点来实现，使得尾数除以基数后大于等于1但小于基数。 **单精度**和**双精度**浮点数分别使用32位和64位来存储数值。在单精度中，32位被分为8位阶码、23位尾数和1位符号位；在双精度中，64位则分为11位阶码、52位尾数和1位符号位。 **IEEE754**是浮点数表示的国际标准，定义了浮点数的存储格式、运算规则以及异常处理等。它确保了不同系统间的浮点数计算一致性，支持规格化、非规格化数、无穷大、NaN（非数字）等多种情况。 理解这些基础知识对于深入学习计算机体系结构、编译器设计和数值计算等领域至关重要。浮点运算虽然复杂，但通过IEEE754标准，我们可以有效地处理和存储现实世界中广泛存在的连续数值。