离散结构算法解析：线段树与树状数组在动态统计问题中的应用

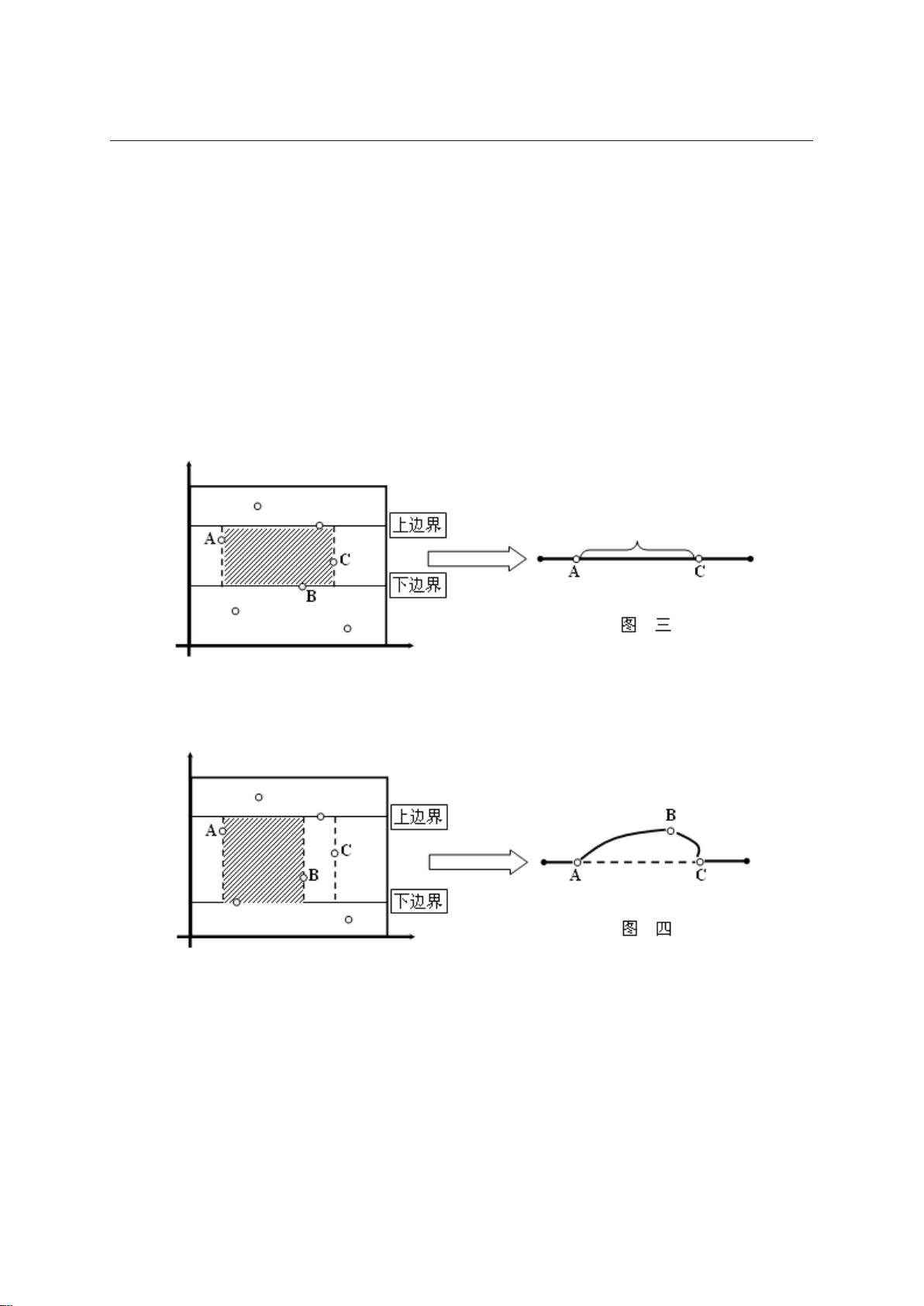
"《算法艺术与信息学竞赛》学习指导(下)涵盖了离散结构上的算法，特别是关于序列上的问题，如线段树和树状数组的深入探讨，以及动态统计问题的解决策略。" 在《算法艺术与信息学竞赛》的学习指导下，第六章主要关注在离散结构上应用的算法，这些结构包括序列、树、图和字符串等。离散结构具有独特的数学特性，从而催生出一系列创新算法。本部分特别强调了序列上的算法，虽然序列结构相对简单，但其相关的算法设计往往充满智慧。 6.1节中，介绍了序列上的问题，包括排序、统计问题以及序列数据结构的应用。线段树和树状数组作为重要的数据结构在此被提及。线段树是一种由区间不断二分得到的树形结构，它反映了分治算法在处理区间问题时的思路。如图8.1所示，线段树将区间[1,10]分割成单个点，具备以下特点： 1. 每一层都是区间[a,b]的一个划分，长度为L=b-a。 2. 树有log2L层。 3. 从根节点到任意叶节点p的路径表示的所有区间都包含点p，且其他区间不包含p。 4. 对于区间[l,r]，可以将其分解为不超过2log2L个不相交线段的并。 基于这些特点，线段树支持快速的区间查询和修改操作。对于修改一个点，仅需更新log2L个树中区间；统计区间和，需要累加2log2L个树中区间，两者的时间复杂度均为O(logn)。 接着，书中的动态统计问题I展示了线段树在处理动态数组查询和修改的效率。在直接操作数组的情况下，修改元素是常数时间，但区间和的查询可能达到O(n)。而使用线段树，修改和查询的时间复杂度均降低到O(logn)，显著提高了性能。 动态统计问题II引入了区间加法操作，即给区间[l,r]内的所有数同时加d。这个问题同样可以通过线段树优化，确保修改和查询操作的时间复杂度保持在O(logn)。 通过以上内容，我们可以看出《算法艺术与信息学竞赛》的学习指导(下)在离散结构和序列算法上的深入讲解，提供了高效处理动态统计问题的方法，这对于信息学竞赛和实际编程问题的解决具有很高的参考价值。学习这部分内容，不仅可以提升算法设计能力，还能增强解决实际问题的技巧。