奇异性和幂几何在多尺度Feynman积分区域展开的应用
72 浏览量
更新于2024-07-16
收藏 1.35MB PDF 举报
"这篇论文是关于在多尺度Feynman积分中展开区域的研究，主要涉及奇异性、幂几何图形以及Landau方程的应用。研究人员提出了一种新颖的方法，通过考虑奇点和与之相关的Landau方程来解决区域识别问题。文章详细介绍了如何在区域方法的框架内运用这种方法，并通过Power Geometry技术对小阈值参数进行扩展来分析Landau方程。此过程涉及到Newton多面体的分析，该分析借助于Mathematica的凸包程序进行。此外，Landau方程的Gröbner基础元素也用于揭示不同的积分区域，如势能区域和Glauber区域。为了验证和基准测试这个方法，研究者使用名为ASPIRE的算法对一系列单循环和双循环示例进行了研究。"
这篇论文的核心知识点包括：
1. **多尺度Feynman积分**：在粒子物理学中，Feynman积分是计算量子场论中的散射振幅的关键工具，特别是在处理多个能量尺度的问题时。多尺度问题往往导致复杂的积分，需要特别的处理方法。
2. **奇点分析**：在Feynman图中，奇点对应于物理过程中的不连续性或分支点。理解奇点有助于确定积分的复杂性，这对于确定积分的有效区域至关重要。
3. **Landau方程**：由Landau提出的这些方程描述了在Feynman积分中可能出现的奇点配置。这些方程对于识别积分可能遇到的困难区域非常有用，比如在哪里可能会发生分支切割或发散。
4. **幂几何图形（Power Geometry）**：这是一种数学工具，通过扩展小阈值参数来分析方程，帮助理解和简化高维度问题。在这个研究中，它被用来分析Landau方程并揭示积分的结构。
5. **Newton多面体**：在代数几何中，Newton多面体与多项式系统的系数相关联，它可以提供关于系统解的信息。在本文中，Newton多面体的分析帮助评估积分区域的边界。
6. **Mathematica软件**：一种强大的数学计算软件，被用来实现Newton多面体的计算和分析，显示了理论研究与现代计算工具的结合。
7. **Gröbner基础**：在代数学中，Gröbner基是用于解决多元多项式方程组的一个工具。在Landau方程的背景下，它可以提供一组转换，这些转换有助于揭示积分的特定区域。
8. **ASPIRE算法**：这是研究中使用的一种算法，用于研究和基准测试提出的区域识别方法。它被应用于单循环和双循环的示例，以验证新方法的有效性。
9. **区域方法**：这是解决多尺度问题的一种策略，它将积分分解为不同的区域，每个区域对应于特定物理过程的主导贡献。
10. **势能区域和Glauber区域**：在粒子碰撞中，势能区域通常对应于低能量交换，而Glauber区域则涉及非弹性散射。通过Gröbner基础的元素，研究者能够识别出这些特定的物理区域。
这项研究提供了一个新的技术，用于在多尺度Feynman积分中有效地识别和处理复杂的积分区域，这对理解和计算高能物理中的复杂过程有着重要的意义。
57 Page 4 of 20 Eur. Phys. J. C (2019) 79 :57
0.0 0.5 1.0 1.5 2.0 2.5 3.0
0.0
0.2
0.4
0.6
0.8
1.0
x
1
Fig. 2 Convex hull of the projected set of vector exponents
In the following sub-sections we will demonstrate a new
way of solving the problem of finding regions based on the
singularities of Feynman integral in Alpha representation.
2.3 Determination of the regions using the analytic
structure of the propagator
The different regions, where a particular mass or kinemati-
cal scale becomes important can be linked to the underlying
singularities of the Feynman integral. In the following, we
will introduce the main concepts and motivate the ideas that
will lead to the development of the final algorithm. We first
give an overview of the singularities that are of interest for
our problem, followed by a review of the basic understand-
ing of particle thresholds as pinched singularities
in momen-
tum space. This interpretation is well understood and can be
mathematically expressed using a set of equations called the
Landau equations. Since expansions in the neighborhood of
the singular surfaces give us the leading order behavior of
Feynman amplitudes, we perform similar expansions in the
Alpha-parameter space in carefully chosen neighborhoods of
the singular points. This requires us to use techniques from
the field of power geometry. We then motivate the use of
Gröbner basis for the identification of all neighborhoods of
the singular points.
2.3.1 Singularities and threshold processes
Understanding the analytic structure of the amplitude is cru-
cial to identifying the different regions. The poles in the inte-
grand of the amplitude for a given process are functions of
kinematical invariants, loop momenta etc. Therefore, when
these parameters vary, the poles in the integration domain
move. In the case of isolated singularities, it is always pos-
sible to deform the contour of integration to avoid these sin-
gular points. However, sometimes, the poles migrate so as to
pinch the contour of integration (pinch singularities) or move
to one of the end point of the integration (end point singular-
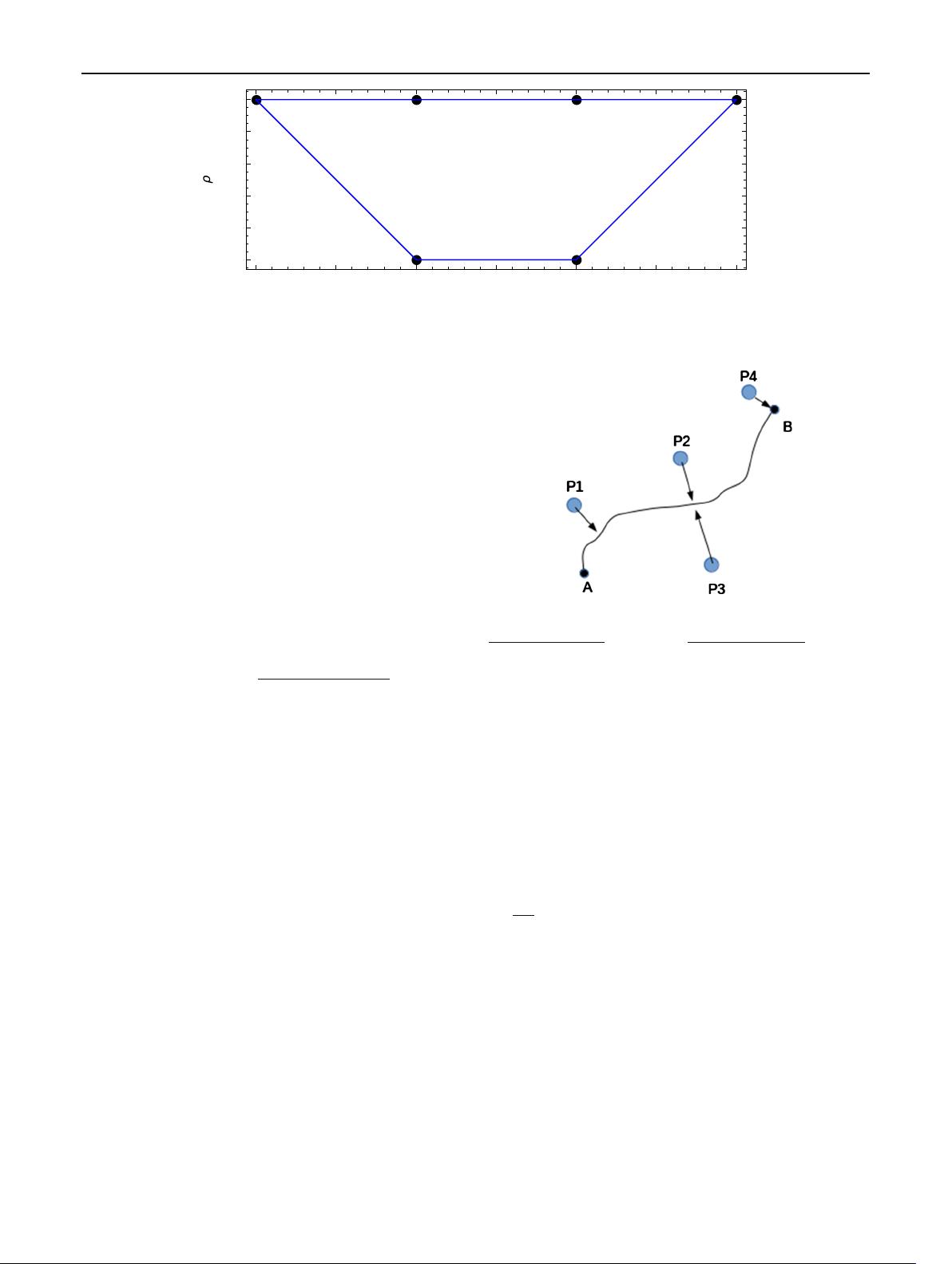
Fig. 3 Types of singularities: P1 is a simple pole, P2 and P3 are
Pinched Singularities
and P4 is an End Point Singularity. While the
contour between the points A and B can be deformed so as to avoid
the simple pole P1, the same is not true for the pinch and end-point
singularities
ities) as illustrated in Fig. 3. In such cases, these singularities
cannot be avoided by contour deformations.
The condition for a point to be one of these unavoidable
singular points is the usual condition for establishing a singu-
larity for a polynomial. For an arbitrary polynomial g({x
i
})
that appears in the denominator of the Feynman integral, the
point x
i
is singular point iff
g({x
i
}) = 0,
∂g
∂x
i
= 0. (9)
Therefore, at these unavoidable singular points, hereby
referred to as just singular points, the integrand diverges. We
will now adopt the approach of Coleman and Norton [25],
also discussed in [26], to explain the connection between the
singularities and physical events.
Consider a general Feynman amplitude in the Alpha rep-
resentation
I =
i
d
d
k
i
j
dα
j
δ
⎛
⎝
j
α
j
− 1
⎞
⎠
f ({q
j
}) D
−n
(10)
123
剩余19页未读，继续阅读
2020-04-01 上传
2020-03-23 上传
2020-03-27 上传
2024-11-03 上传
2024-11-03 上传
2023-07-27 上传
2023-09-17 上传
2024-11-09 上传
2024-08-27 上传
