自动控制原理第三章：闭环传递函数与动态性能分析

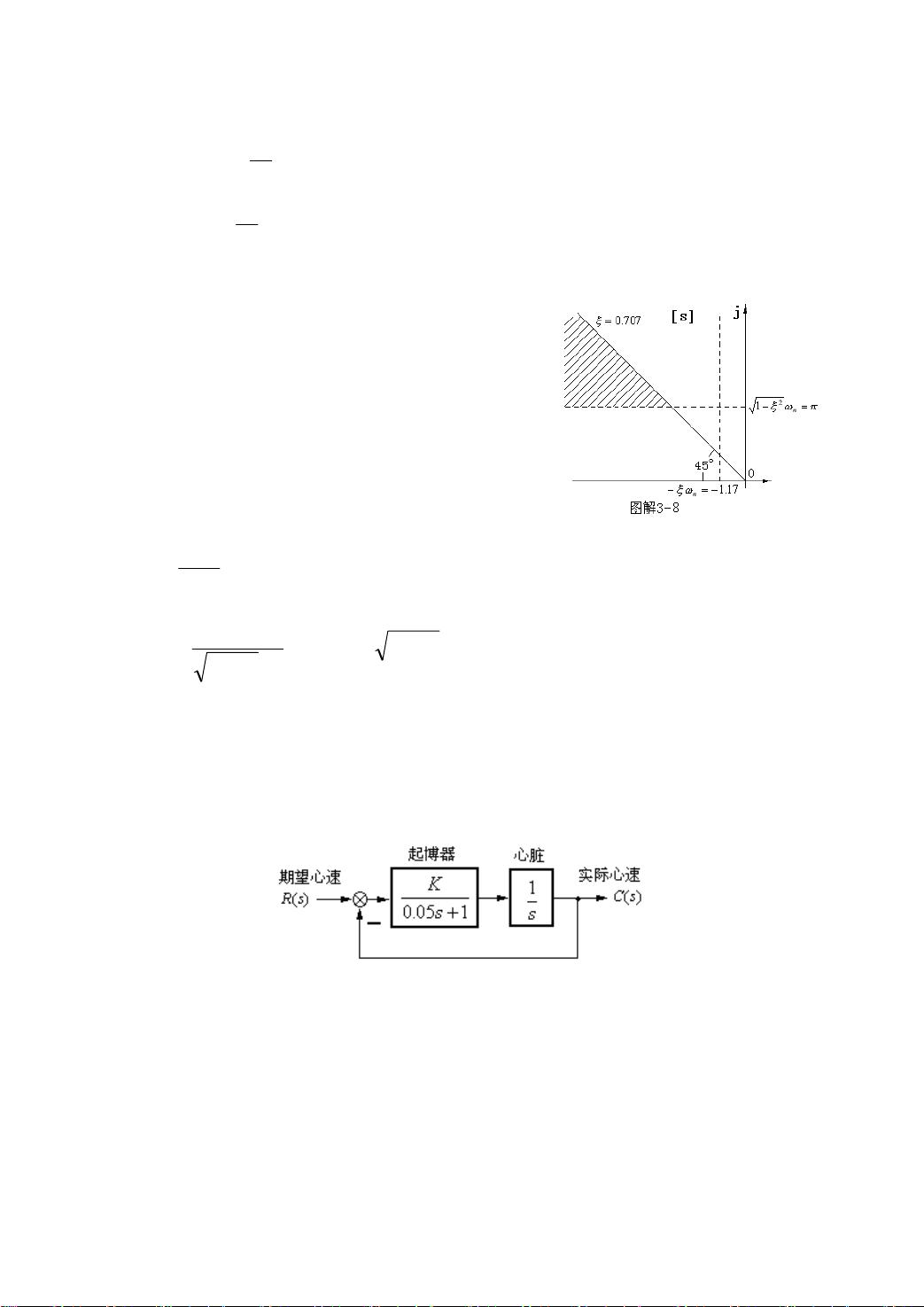
本资源主要涉及自动控制原理第三章的内容，包括习题解答和重点难点分析。章节中的问题涉及闭环传递函数的求解、高阶系统的一阶微分方程近似及其动态性能指标、单位阶跃响应的计算以及一阶系统结构的分析。 在第3-1题中，给出了一个系统脉冲响应，要求求出该系统的闭环传递函数Φ(s)。根据题意，系统的闭环传递函数可以通过脉冲响应与零初始条件下的拉普拉斯变换相结合来得到，即Φ(s) = L{ekt}(s)/L{δ(t)}(s)。计算得出的结果是Φ(s) = (1 + 0.125s)/(s^2 + 0.25s + 0.125)。 第3-2题讨论了一阶微分方程对高阶系统动态性能的影响。题目要求证明，对于满足0<(T-τ)<1的系统，其动态性能指标可以通过一阶微分方程的特征参数T来描述。单位阶跃响应下，输入和输出之间的关系表明了系统的上升时间td、峰值时间tr以及衰减振荡周期ts。通过计算得出，tr(T) = ln(2)/T和tsT = T/ln(3)，分别对应于阶跃响应从0.1到0.9所需的时间和半衰期。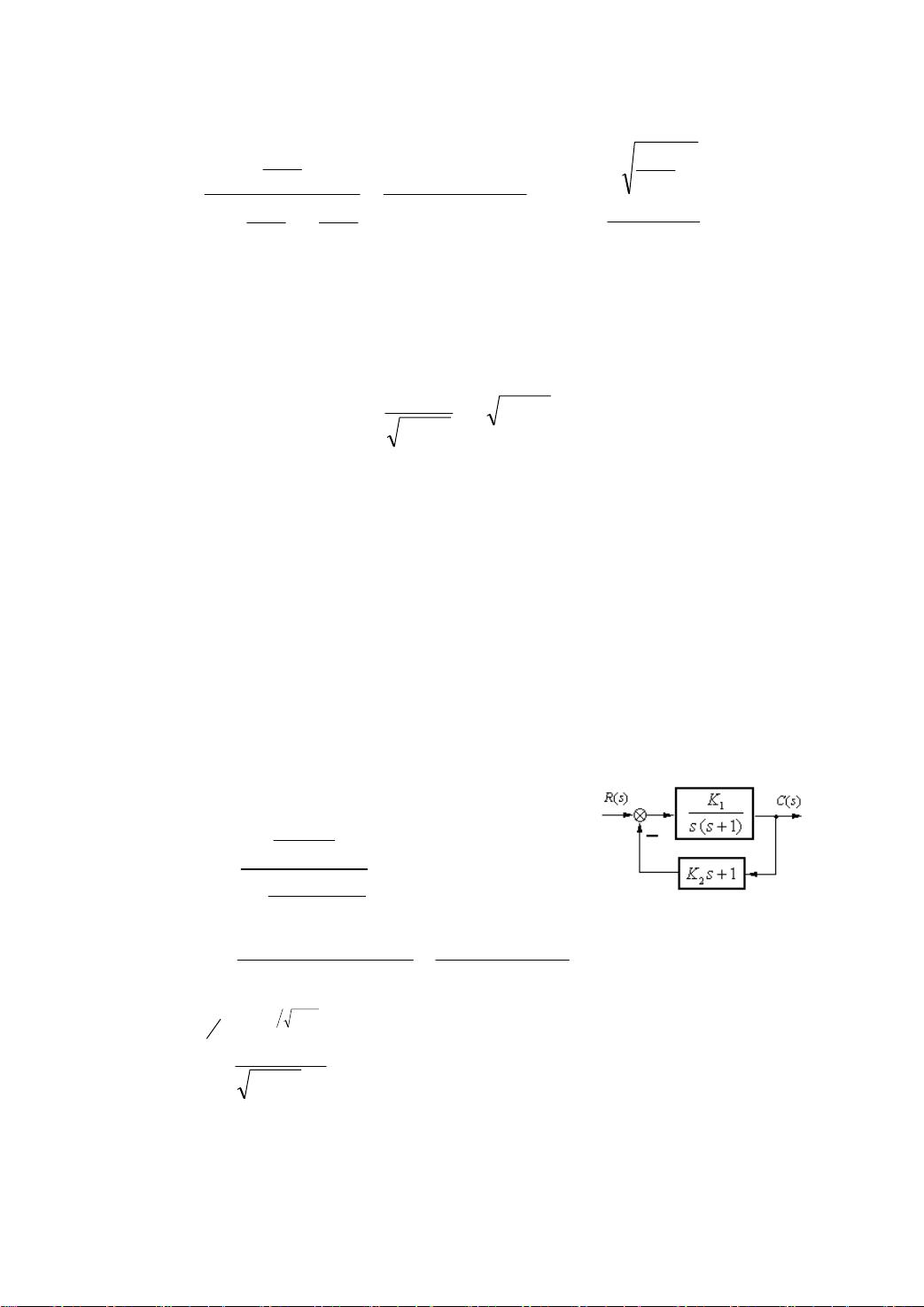 第3-3题涉及一阶系统的结构图，需要确定闭环增益和调节时间。一阶系统通常由比例积分控制器（PI）组成，增益K和积分时间Ti决定了系统的响应速度。根据系统结构图，可以通过计算或解析方法确定这些参数，但具体数值未给出。调节时间τc通常定义为输出信号达到稳态值90%所需的时间，与系统参数紧密相关。 这些习题展示了自动控制原理中的关键概念，如系统函数的求解、动态性能的定量分析以及一阶系统的设计与分析。理解并掌握这些问题对于深入理解自动控制系统的工作原理和设计至关重要。通过解决这些问题，学生可以提升对控制系统稳定性、响应时间和控制策略的理解，为实际工程应用打下坚实的基础。