图数据结构详解：最小生成树与最短路径算法

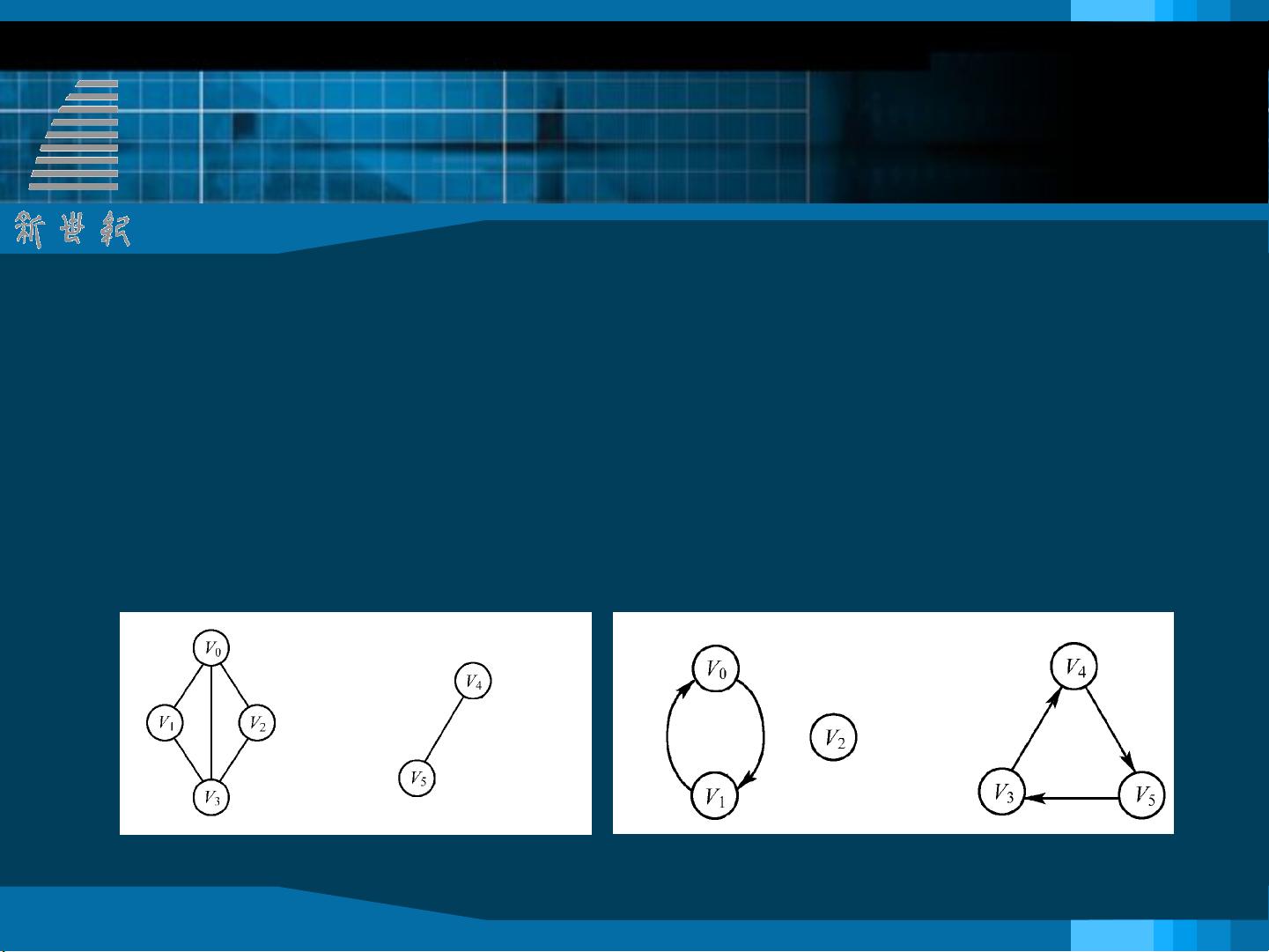
"本资源为数据结构第六章关于图的教程，主要涵盖了图的基本概念、存储结构、遍历方法、最小生成树算法（包括普里姆和克鲁斯卡尔）、最短路径算法（迪杰斯特拉和弗洛伊德）、拓扑排序以及关键路径等内容。" 在数据结构中，图是一种非常重要的抽象数据类型，它用于表示对象之间的关系。图由顶点（vertices）和边（edges）构成，顶点代表数据元素，边则表示它们之间的关系。根据边的方向，图可以分为两类：无向图和有向图。无向图中的边不具有方向性，而有向图中的边则具有方向，通常用箭头表示。 图的基本术语包括： 1. 完全图：在无向完全图中，任意两个不同的顶点之间都有一条边相连；在有向完全图中，每个顶点到其他所有顶点都有一条有向边。 2. 子图：如果一个图B的顶点和边都是另一个图A的顶点和边的子集，那么B是A的子图。 图的存储结构主要有两种：邻接矩阵和邻接表。邻接矩阵是一个二维数组，用来表示图中任意两个顶点之间是否存在边；邻接表则是为每个顶点存储其相邻顶点的链表或数组，更适合表示稀疏图。 图的遍历主要包括深度优先遍历（DFS）和广度优先遍历（BFS）。DFS通过递归或栈来探索尽可能深的分支，而BFS则使用队列来按层次顺序遍历顶点。 最小生成树是图论中的一个重要概念，用于寻找连接所有顶点的边最少的树形子图。普里姆算法和克鲁斯卡尔算法是两种常用的最小生成树算法，前者从一个顶点开始逐步增加边，确保每次添加的边连接的是两个不同连通分量的顶点，后者则是按照边的权重从小到大依次选择边，避免形成环路。 最短路径问题旨在找到图中两点间的路径，使得路径上的边权和最小。迪杰斯特拉算法适用于有向无环图（DAG）且边权重非负的情况，它通过松弛操作不断更新节点到源点的最短距离。弗洛伊德算法则可以处理带负权的边，通过动态规划求解所有节点对之间的最短路径。 拓扑排序是对有向无环图进行排序的一种方法，结果是一组顶点的线性序列，其中对于图中的每一条有向边uv，顶点u都在顶点v之前出现。关键路径是项目管理中的概念，表示从项目开始节点到结束节点的最长路径，决定了项目的最短完成时间。 学习这些内容对于理解和解决复杂问题，如网络路由、社交网络分析、算法设计等具有重要意义。通过深入理解并熟练掌握图的相关知识，可以为编程和算法设计提供坚实的基础。