系统工程导论：Matlab实现线性回归与置信区间分析

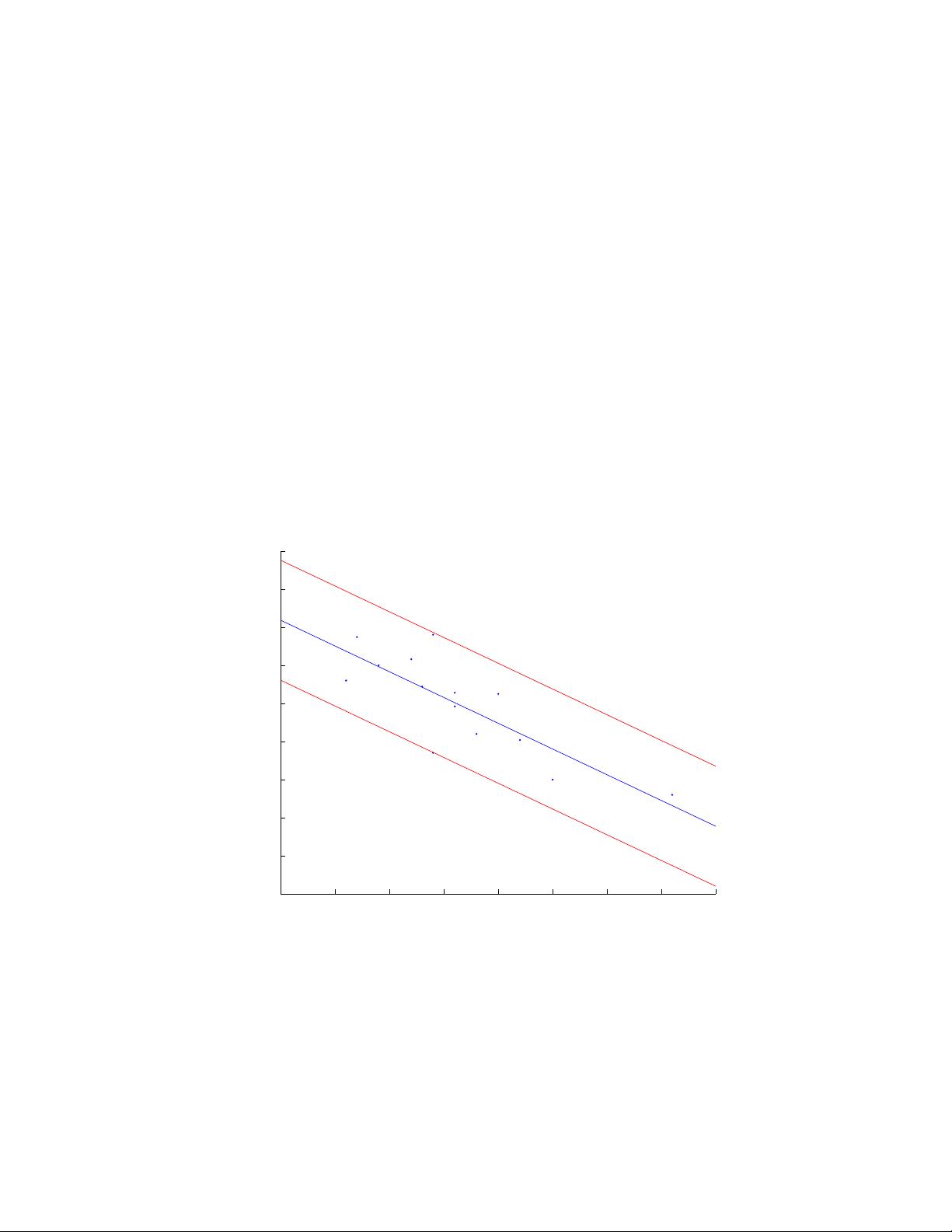
本次作业是关于系统工程导论中的回归分析部分，具体涉及Matlab软件的应用。作业由何舜成在2015年4月19日完成，内容围绕数据分析和线性回归模型的构建。以下是关键知识点的详细解析： 1. 数据分析与回归直线：作业中使用了14个数据点，这些数据表示的是Proportion of X Element和Proportion of Y Element之间的关系。通过运行Matlab代码，得到了回归直线的方程y = 5.180451 - 135.071531x，这个方程展示了变量X对Y的线性预测效果。同时，还有两个边界方程y = 6.755133 - 135.071531x和y = 3.605768 - 135.071531，用于定义置信区间。 2. 置信区间的评估：13个数据点位于回归直线附近，表明回归线能够较好地描述数据分布。只有一个点稍微超出置信区间边界，这可能需要进一步检查是否存在异常值或测量误差。 3. F检验与假设检验：通过计算F统计量（F = (N-2)ESS/RSS），发现其值为22.5791，显著性水平α被设定为0.05。根据给定的临界值Fα=4.7472，由于F>Fα，作业者拒绝了原假设H0（即X和Y之间没有线性关系），接受备择假设H1，即两者呈线性关系。 4. Matlab实现：提供的Matlab代码实现了回归分析的全过程，包括数据输入、绘图（散点图）、计算平均值、回归线的计算以及F检验的执行。代码中的关键步骤包括计算X和Y轴的数据、创建散点图、确定回归方程、以及执行统计检验。 总结来说，这次作业的核心内容是利用Matlab进行线性回归分析，通过实际数据验证了两个变量之间的线性关系，并且进行了统计学上的显著性检验，从而得出有统计学意义的结论。这对于理解系统工程中如何通过数学模型来描述和预测现象，以及运用统计方法验证假设具有重要的实践价值。