离散时间信号与系统复习：关键概念与应用探讨

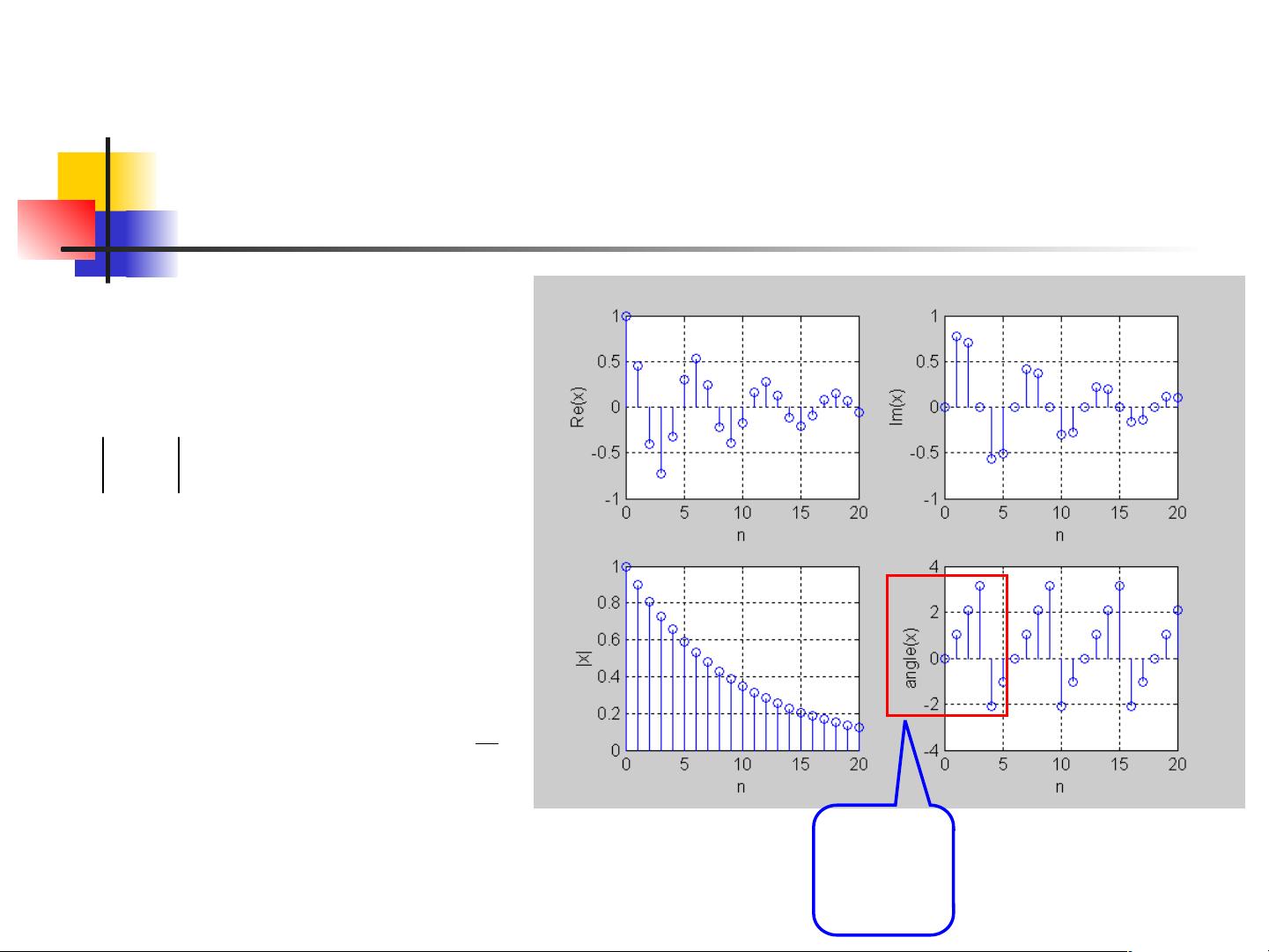
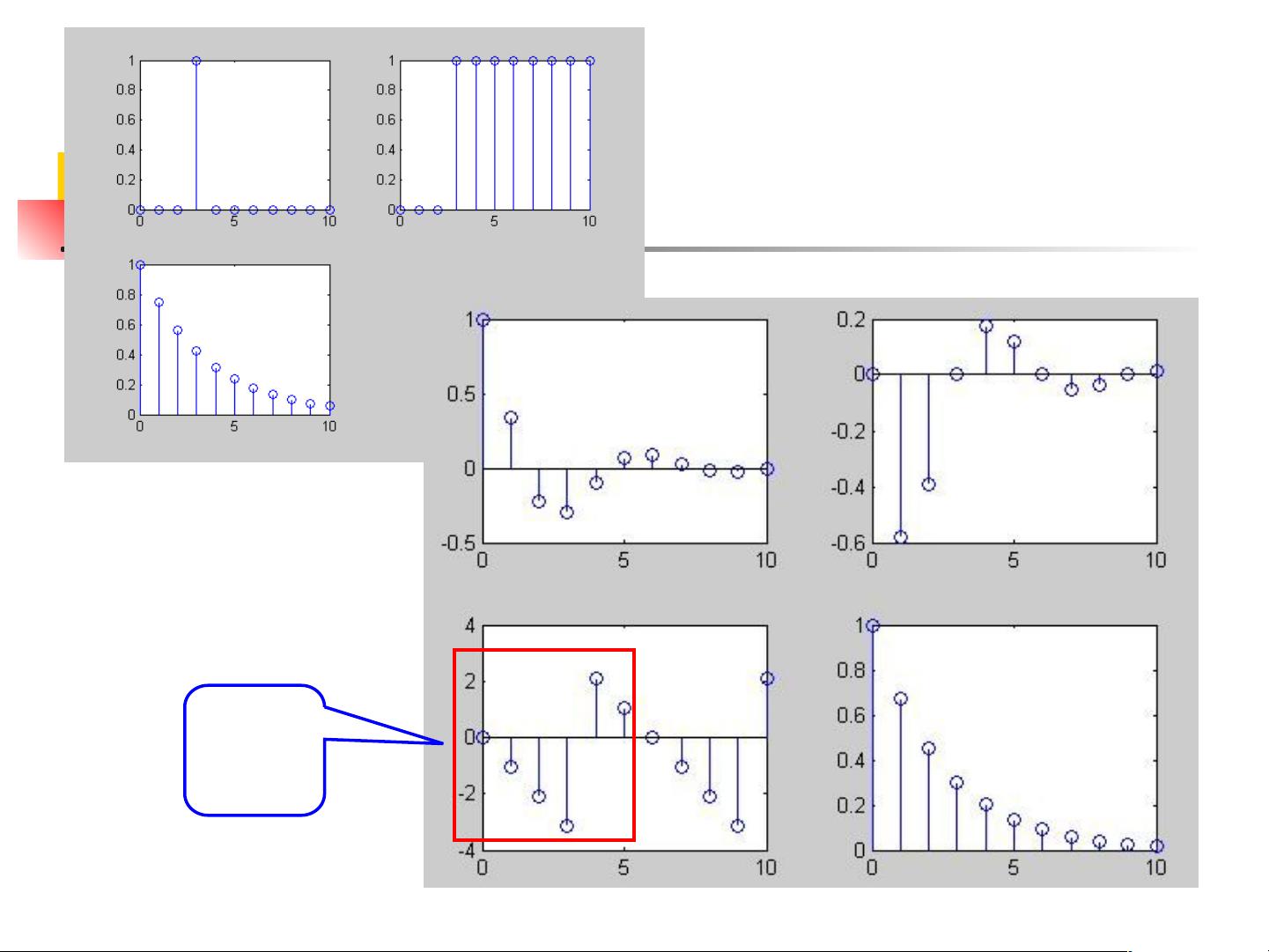
本章主要探讨离散时间信号与系统的基本理论，它是数字信号处理领域的基石。首先，引言部分强调了这一主题的重要性，指出它对于深入理解数字信号处理至关重要，并提出了几个关键问题作为学习和复习的线索。 1.1 离散时间信号 离散时间信号通常以序列的形式表示，即{x(n)}，其中n为整数，每个x(n)代表信号在时间上的一个采样值。序列可以是实数或复数。序列{x(n)}的性质包括：x(n)仅在n为整数时有意义，其复共轭序列表示为{x*(n)}；x(n)实际上是信号在时间间隔T下的采样值，这些值在存储中按顺序排列。 1.1.1 常见典型序列 - 单位脉冲序列（离散冲激）δ(n)：在离散域中，δ(n)类似连续时间的单位冲激函数δ(t)，但它是集中在n=0点的序列，而不是函数。尽管在数学上是极限定义，但对于实际计算，δ(n)在n=0处取值为1，方便处理。 - 单位阶跃序列u(n)：在离散时间中，u(n)对应于连续时间的单位阶跃函数u(t)，同样在n=0处可能没有明确定义。 本章接下来会深入讨论采样过程，以及如何将连续时间信号转换成离散时间信号。离散时间信号的傅里叶变换和Z变换是分析信号频率特性的重要工具，它们分别对应于连续时间信号的傅立叶变换和拉普拉斯变换。此外，还将涉及离散时间系统的概念，包括系统的频率响应和系统函数，这是衡量系统性能的关键指标。 在学习过程中，读者会探索离散时间信号与数字信号的差异，如采样频率的选择，这对信号质量的恢复和处理效果有直接影响。同时，还会关注离散系统在计算机中的实现，比如如何利用数字信号处理器(DSP)进行信号处理，并讨论因果稳定性在数字信号处理中的意义，以及可能影响稳定性的因素。 通过本章的学习，学生不仅能复习基础理论，还能为后续章节探讨更复杂的技术打下坚实基础。在解答这些问题的过程中，读者将深化对离散时间信号与系统概念的理解，从而提升在数字信号处理领域的实践能力。