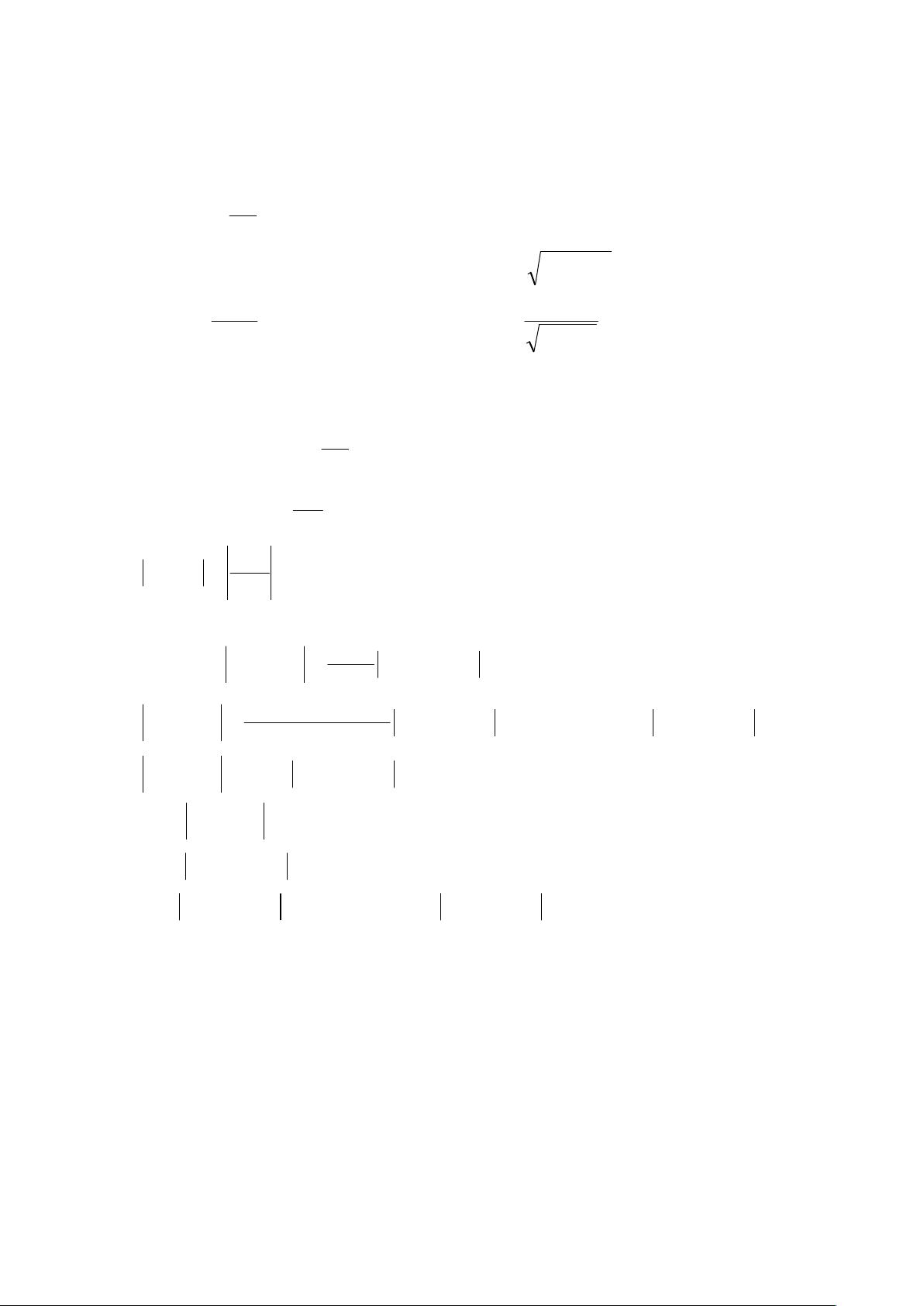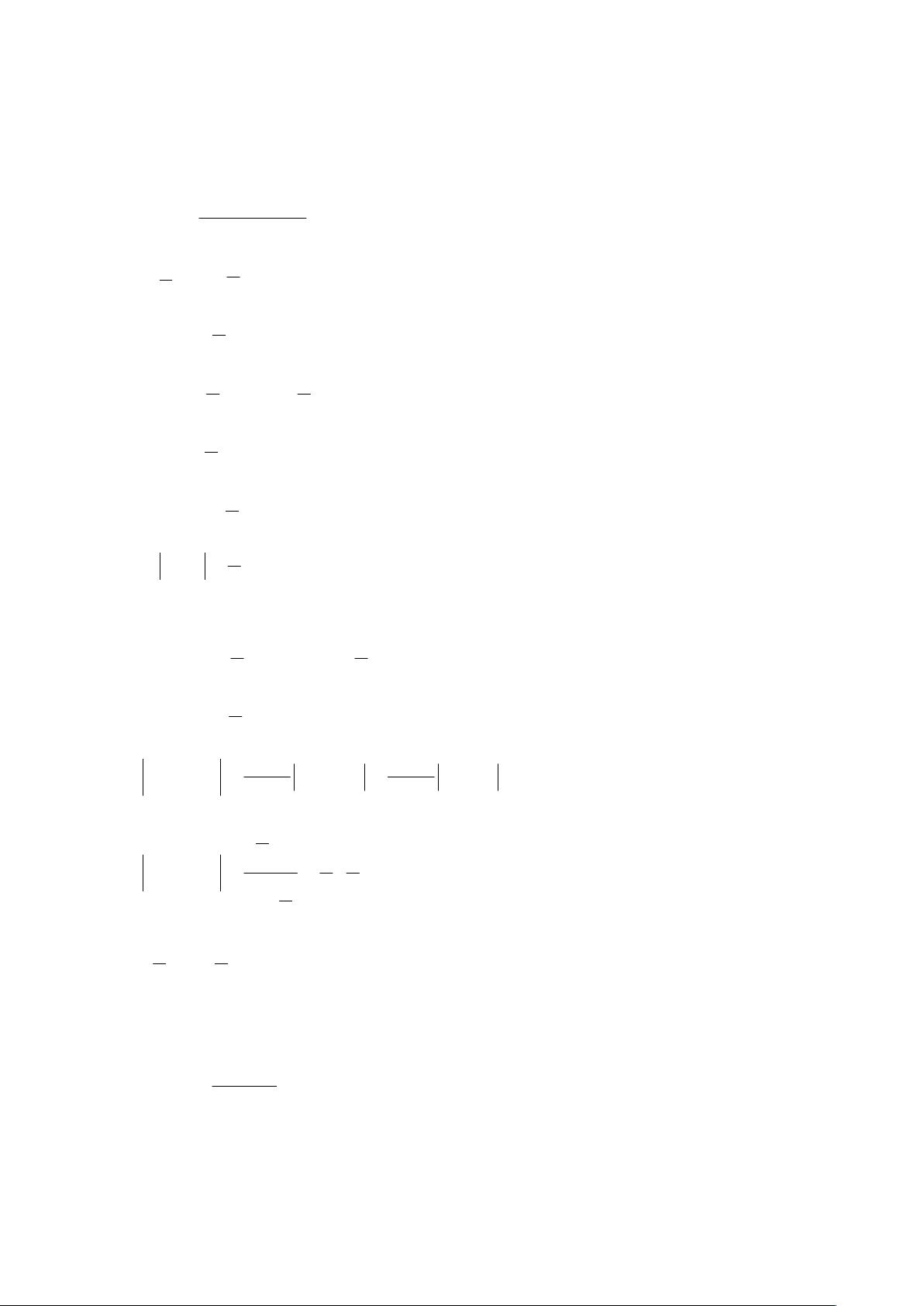数值计算稳定性分析与Matlab应用

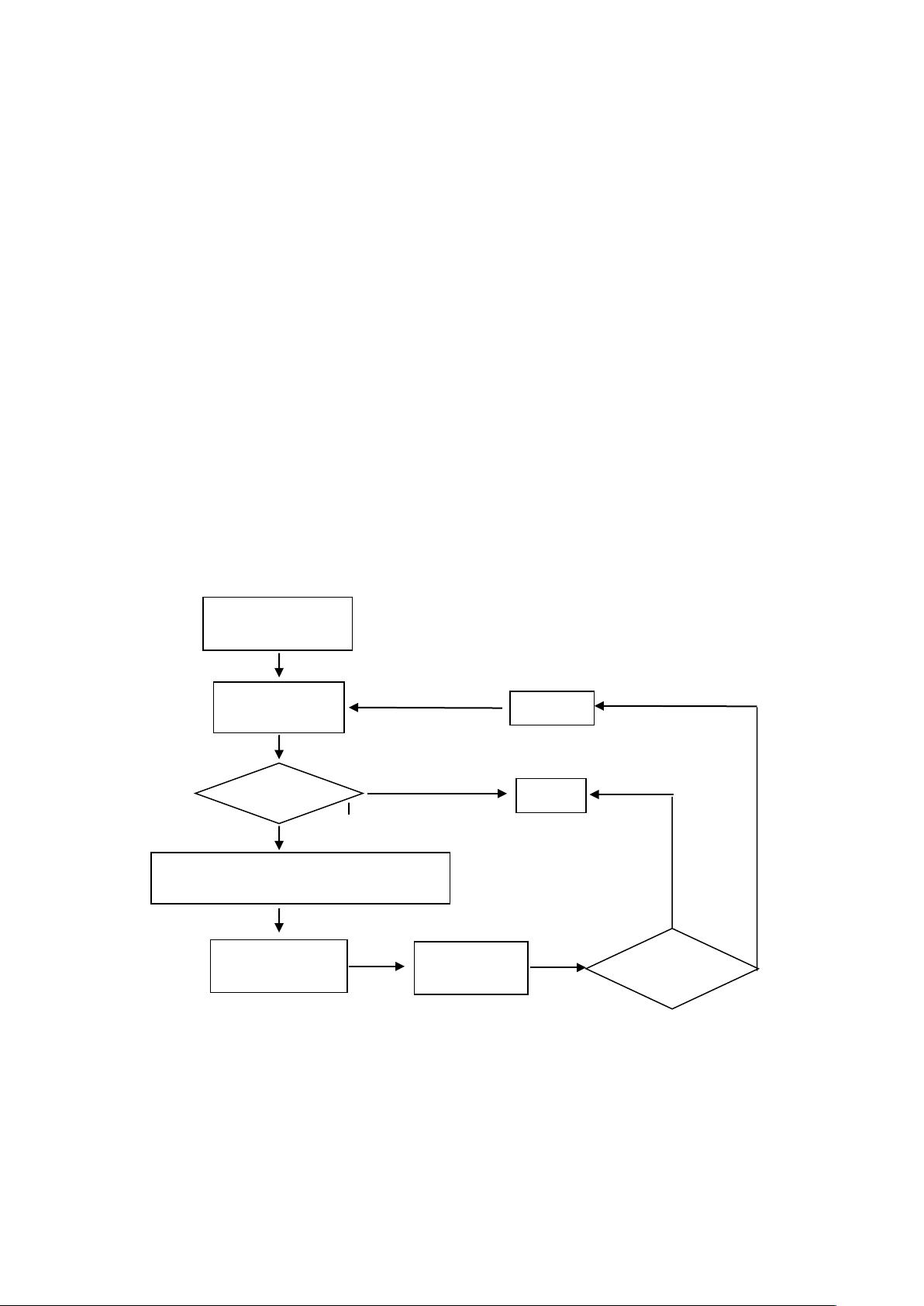
"数值计算与Matlab语言金一庆课后答案.doc" 在数值计算领域，稳定性和精度是至关重要的考量因素。文档中的内容涉及到这些问题，通过具体的数学问题展示了计算过程中的不稳定性以及误差分析。 首先，第一题讨论了一个递推关系[pic]，其中n表示迭代次数。题目给出了两组不同的初始条件[pic]和[pic]，并计算了四次迭代的结果。随着n的增加，尽管初始值相差不大，但结果[pic]的差异迅速增大，这表明该递推公式对于计算是不稳定的。这种不稳定性的出现是因为在数值计算中，小的误差会随着迭代的进行被放大，导致最终结果的巨大差异。 第二题涉及递推公式[pic]和误差分析。当y0=28，并采用五位有效数字时，每次递推都有一个误差[pic][pic]。这意味着每次迭代，结果的有效数字都会减少，计算y100后的误差累积会导致只有两位有效数字留存。 第三题中，函数[pic][pic]的求值问题引入了对数和开方的误差。如果使用六位函数表求对数，误差可能会达到[pic]，即大约0.5乘以10的负四次方。通过使用不同的等价公式[pic]，可以计算出新的对数误差，此处为[pic]，即大约0.5乘以10的负四次方。这说明即使在计算过程中使用不同的方法，误差也是不可避免的。 第四题关注的是基于有效数字的误差估计。对于函数f=sin[(3.14)(2.685)]，我们可以通过分析每个因子的误差来估计f的绝对误差限和相对误差限。假设x*=3.14，y*=2.685是精确值，E(x)和E(y)分别是它们的误差，这里分别是0.5乘以10的负二次方和0.5乘以10的负三次方。计算出sin(x*y*)=0.8，然后根据误差传播定律，我们可以估算出f的误差范围。 这些习题突出了数值计算中的关键概念，包括递推公式的稳定性、误差的累积与传播、有效数字在计算中的影响，以及不同计算方法对误差控制的作用。在使用Matlab或其他数值计算工具时，理解和掌握这些原理对于获得准确可靠的计算结果至关重要。