Hopfield神经网络：理论与应用

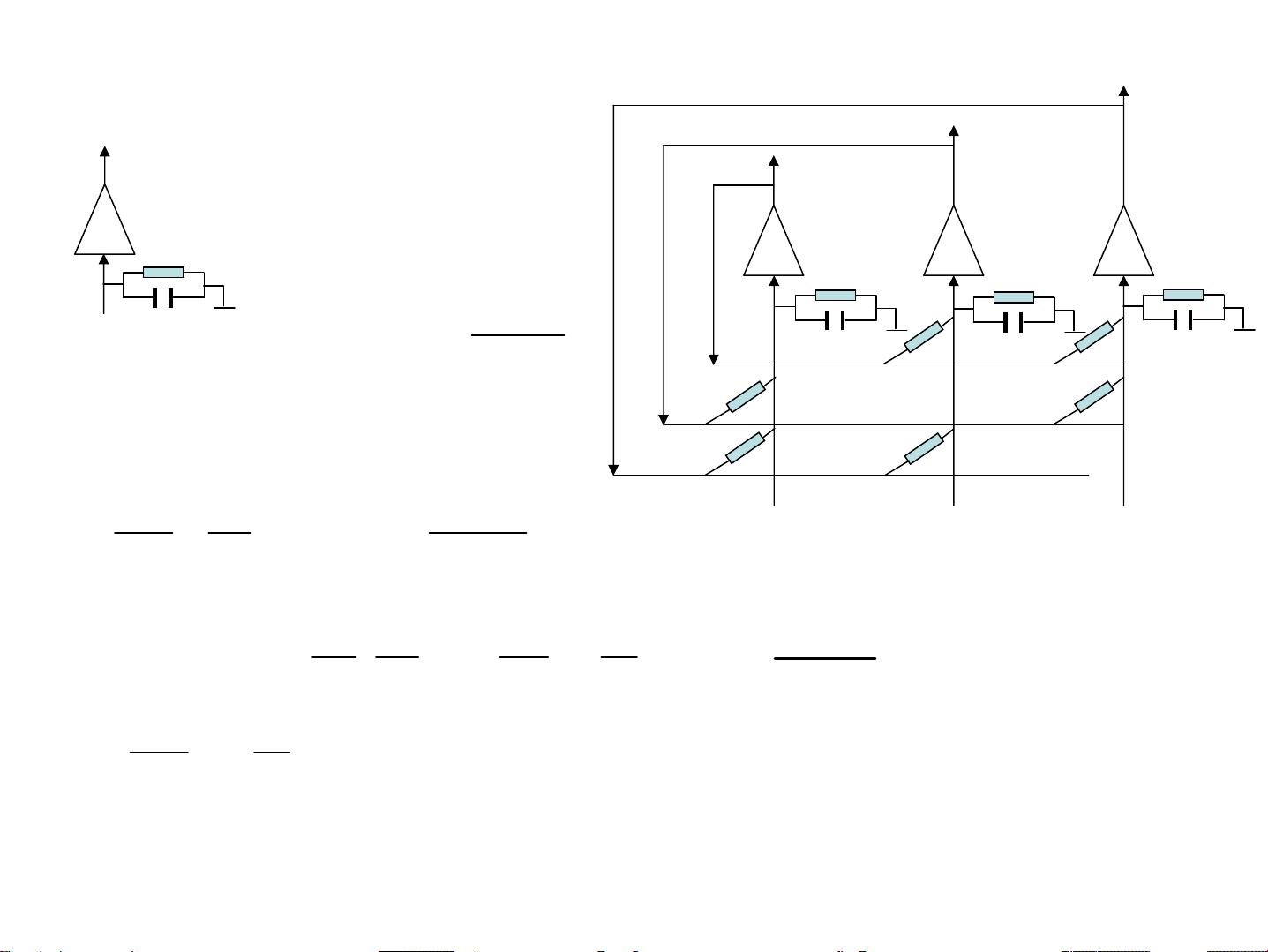
" Hopfield 神经网络是神经网络的一种，主要用于模式识别和联想记忆。它由John J. Hopfield在1982年提出，是一种反馈神经网络，其结构和运作机制受到生物大脑神经元网络的启发。 Hopfield 网络的工作原理基于能量函数，能够通过迭代更新来稳定在特定的状态，这些状态可能对应于存储在权重矩阵中的模式。” Hopfield神经网络主要分为离散型和连续型，本描述主要关注离散型。离散型Hopfield网络的基本公式是一个阈值函数，其中sgn表示符号函数，wij是神经元i到神经元j的连接权重，Ii是外部输入，xt是神经元i在时间步t的激活状态。在网络模型中，每个神经元的状态可以是+1或-1，权重wij定义了神经元之间的相互作用强度。 Hopfield网络有两种工作方式：同步方式和异步方式。在同步方式下，所有神经元在同一时间更新状态；而在异步方式中，每次只有一个神经元更新，其他神经元保持不变。能量函数（Lyapunov函数）L是Hopfield网络稳定性的关键，它表征了网络状态的“能量”，当网络状态不再变化时，能量达到最小，此时的状态被认为是稳定点。 稳定点是Hopfield网络从任意初始状态经过有限时间后，状态不再改变的状态。如果网络以异步方式工作且权矩阵的对角元素为0（或为负值），系统总会收敛到稳定状态。在同步工作模式下，网络可能收敛到一个稳定状态，也可能收敛到一个Hamming距离小于2的极限环。Hamming距离衡量的是两个向量在对应位置上的差异。 Hopfield网络的稳定性可以通过计算不同状态间的Hamming距离来分析。如果两个稳定状态之间的Hamming距离为3，那么它们被认为是稳定的。权值的设计通常根据给定的样本数据进行，例如，在联想记忆应用中，样本数据被用来初始化权重矩阵，可以通过外积型（相关）权设计方法实现，这种方法考虑了样本向量之间的相似性。 Hopfield神经网络是一种利用动态系统理论和能量函数来模拟大脑记忆功能的模型。它在模式识别、优化问题和联想记忆等领域有广泛的应用。通过调整权重和工作模式，网络可以收敛到预设的稳定状态，从而实现对信息的存储和检索。然而，Hopfield网络也存在一些局限性，如可能陷入局部极小值而非全局最优解，这在解决复杂问题时需要谨慎处理。