吴程锴的第四次上机作业：PCA与NMF在高维数据可视化中的应用

"本次上机作业是关于吴程锴同学的第四次作业，主要涵盖了两个部分：PCA（主成分分析）实现高维数据可视化以及降维技术NMF（非负矩阵分解）的应用。作业展示了相应的代码实现和结果展示。" 在第一次作业中，吴程锴同学实现了PCA（主成分分析）来对鸢尾花数据集进行降维并可视化。PCA是一种常用的数据分析方法，它通过线性变换将原始数据转换到一个新的坐标系统中，使得新的坐标系的第一轴（主成分）最大化了数据的方差，第二轴保留尽可能多的剩余方差，以此类推。在这个例子中，目标是将鸢尾花数据集的四维特征降到二维，以便于在二维平面上可视化。 代码中，首先导入了必要的库，包括matplotlib.pyplot用于绘制图形，sklearn.decomposition的PCA模块，以及sklearn.datasets的load_iris函数来加载鸢尾花数据集。数据集的标签（y）和特征（x）被提取出来。然后，PCA对象被创建，设置保留的主成分为2。通过fit_transform方法，原始数据被转换为新的低维表示。接着，根据鸢尾花的三个类别，将降维后的数据分别存储为红色、蓝色和绿色点的坐标。最后，使用scatter函数绘制出不同类别的点，红色用'x'标记，蓝色用'D'标记，绿色用'.'标记，以展示二维空间中的分布。 1.2的结果部分应显示了不同类别的鸢尾花在二维空间中的分布，通过颜色和形状区分，可以观察到各类之间的聚类情况和可能的边界。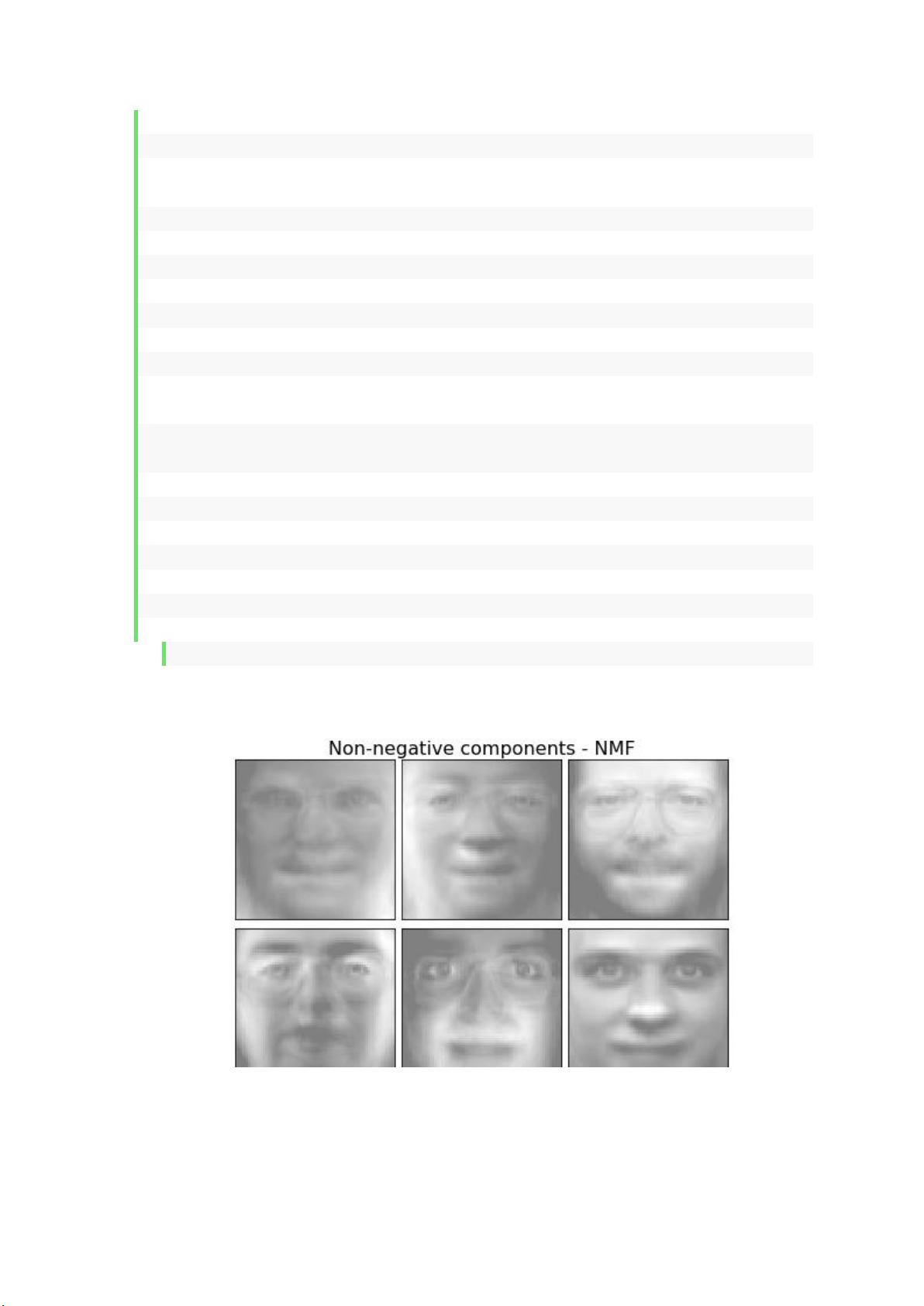 第二个作业涉及的是NMF（非负矩阵分解）。NMF是一种矩阵分解技术，常用于数据挖掘和机器学习中的降维，特别是当数据具有非负属性时。在吴程锴同学的作业中，NMF可能被用来处理如图像数据，例如人脸图像的集合。 2.1的代码部分应该是实现NMF并展示结果的代码，但由于提供的内容不完整，无法具体解析其细节。通常，NMF会将一个非负的输入矩阵W分解为两个非负矩阵H和W，其中H代表特征基，W代表特征系数。在图像处理中，这可以帮助识别和提取人脸图像的潜在特征。 总结来说，吴程锴同学在这次上机作业中展示了对两种重要降维技术的理解和应用：PCA用于高维数据的可视化，NMF则用于非负数据的分解和特征学习。这两个技术都是数据分析和机器学习领域不可或缺的工具，能够帮助我们更好地理解复杂数据集的结构和模式。