单子与部分求值：构造与性质探索

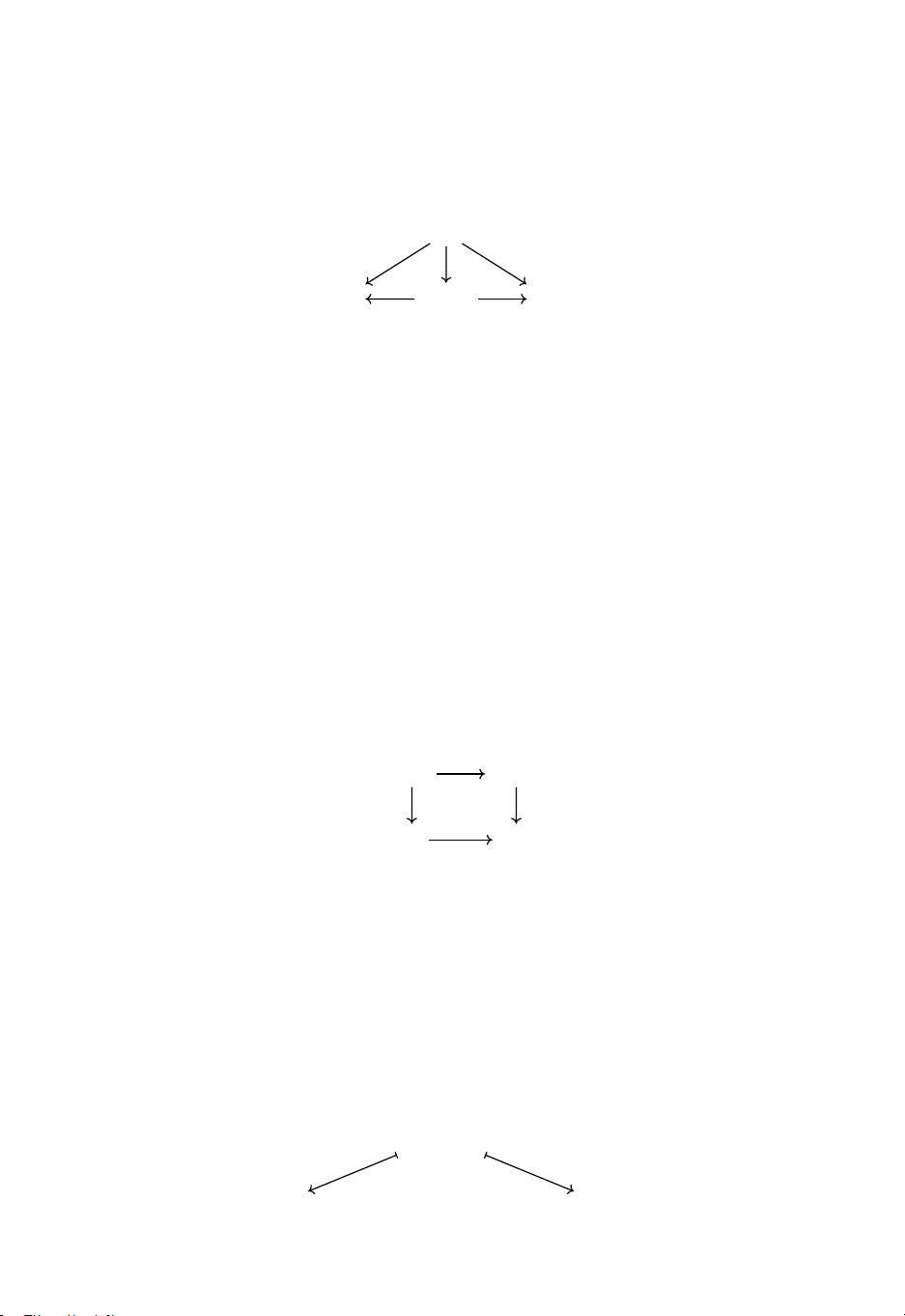
"单子和部分求值构造的研究" 这篇论文深入探讨了单子和部分求值在理论计算机科学中的应用，特别是在重写系统和替换方法中的角色。单子是一种重要的数学构造，在范畴论中广泛使用，它可以被理解为一种在特定范畴中构造对象的方式，类似于泛代数中的形式表达式。在本文中，单子被用来编码形式表达式或形式运算。 部分求值的概念是表达式计算的一个关键方面，它允许我们预先计算表达式的某些部分，而无需完全求解整个表达式。作者提出了一种通用的构造方法，用于任何单子，将部分求值形式化为“2+3”可以被看作是“2+2+1”的部分求值。这一构造与著名的Bar构造相关联，Bar构造在单纯集理论中有重要地位，这里的部分求值对应于1-胞。 论文还研究了部分求值的性质，特别是当单子满足弱Carbohydrate条件时，部分求值可以通过Kan filler性质组合。在概率单子的上下文中，部分求值与随机变量的条件期望相对应，这部分讨论了概率论中的二阶随机优势。 在重写系统方面，部分求值提供了自反、连续且在单子是弱可迁的情况下传递的抽象约简系统。这为高维重写提供了新的视角，并可能对形式化证明和计算理论有深远影响。此外，本文是关于Bar构造的一般重写解释的正在进行的工作的一部分。 关键词包括：单子、Bar构造、重写、高维重写、单纯集和随机优势。这些关键词揭示了研究的广度，涵盖了从基础数学到概率论和计算理论等多个领域，展示了单子和部分求值在理论计算机科学中的核心地位和跨学科应用。