that the stable throughput region for an infinite population
specified by our condition is consistent with that previously
reported in [20] and [21]. Moreover, we show that the
energy consumption of a single node is dependent on the
aggregate input rate as well as the packet size, and can be
kept small within the stable throughput region.
The rest of this paper is organized as follows. A Markov
chain of HOL packets governed by the 802.15.4 protocol is
proposed to derive the network throughput and packet
service time distribution in Sect. 2. The regions of stable
throughput and bounded mean queuing delay are described
in Sects. 3 and 4 for non-acknowledged uplink traffic and
acknowledged uplink traffic, respectively. Section 5 is
devoted to the analysis of power consumption for each
node. The simulation results and conclusion are provided in
Sects. 6 and 7, respectively.
2 Queuing model of input buffer for IEEE 802.15.4
The aim of this paper is to explore the performance of the
slotted CSMA/CA mechanism of the IEEE 802.15.4 pro-
tocol. We first derive the service time distribution of HOL
packets from a Markov chain with state transitions gov-
erned by the 802.15.4 protocol, and then deduce the stable
conditions of throughput and delay from the queuing model
of input buffer. Finally, the ranges of retransmission factor
that guarantee stable throughput and bounded mean
delay are respectively determined from corresponding
conditions.
2.1 Queuing model of input buffer
The network under consideration is governed by the
802.15.4 protocol with the assumption that the entire
superframe duration is active and no CFPs, because we are
only concerned with MAC performance in the contention
mode. Thus, the channel time is comprised of an uninter-
rupted sequence of backoff intervals as described in
[12–16]. In addition, we assume that the network is syn-
chronized and the channel is slotted with mini-slot size a,
the same length as a CCA slot. Packets can only be sent at
the beginning of each mini-slot.
The input buffer of each node is modeled as a Geo/G/1
queue with Bernoulli arrival process. According to the the-
orem on the superposition of point processes proved in [26],
the aggregate attempts generated by all fresh and re-sched-
uled HOL packets form a Poisson stream with rate G. The
K-exponential backoff algorithm is employed for contention
resolutions in this network. A fresh HOL packet is initially in
phase 0, and the packet is scheduled for retransmission at a
later time if the channel is sensed busy. A backlogged HOL
packet is in phase i if it has encountered busy status i times.
The K-Exponential Backoff algorithm allows an HOL packet
in phase i to retransmit with probability q
i
, for i = 1, …, K,
where 0 \ q \ 1 is the retransmission factor and K is the cut-
off phase. That is, the retransmission probability decreases
exponentially with the number of times sensing busy expe-
rienced by the HOL packet, up to K times.
As described in 802.15.4 protocol, each HOL packet,
either fresh or backlogged, would be transmitted only when
both consecutive CCAs are detected idle. Hence, besides
the successful transmission state (Suc) and the collision
state (Col) for transmission, the HOL packet in phase i can
be in one of two fundamental states: performing first clear
channel assessment state (CCA
1
i
), or second clear channel
assessment state (CCA
2
i
), where i = 0, …, K. The state
transitions of an HOL packet for IEEE 802.15.4 protocol
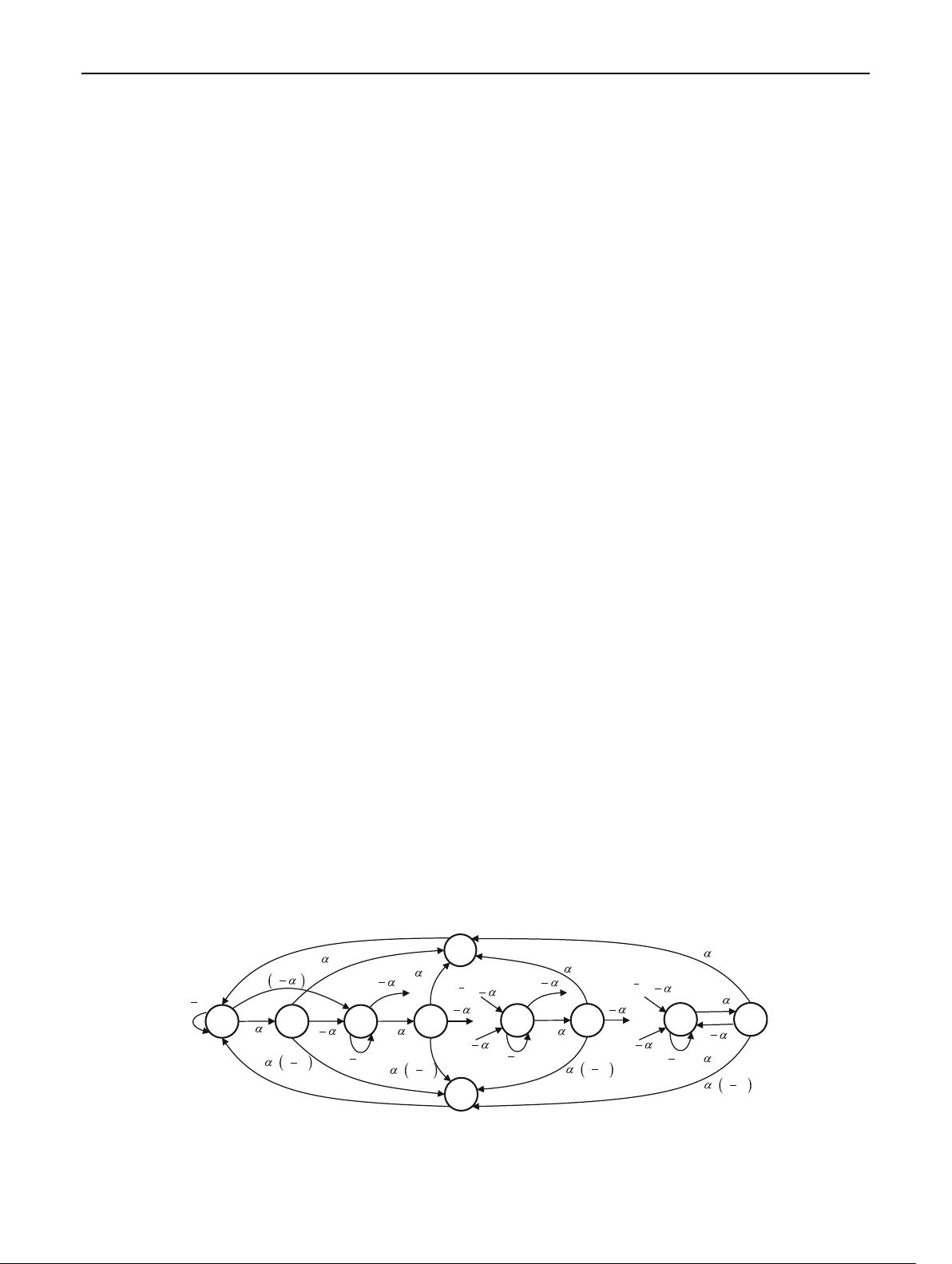
can be described as a Markov chain shown in Fig. 2.
Let a
1
be the probability of assessing channel idle during
first clear channel assessment (CCA
1
), and a
2
be the prob-
ability of assessing channel idle during second clear channel
assessment (CCA
2
), given that it was idle in CCA
1
. The
expressions of these probabilities are given in the following
sections for two different uplink traffic schemes: non-
acknowledgement and acknowledgement, respectively.
Since the transmission of a tagged HOL packet can be
successful only if all other nodes do not send packets in the
same mini-slot. Hence, the probability of successful trans-
mission given that the channel is idle p is shown as follows:
p ¼ e
aG
: ð1Þ
...
1
0
CCA
01
q
2
0
CCA
2
1
CCA
Suc
Col
1
i
CCA
2
i
CCA
...
2
K
CCA
01
1q
2
1
2
1
2
1
2
1
1
1
2
1 p
2
1 p
2
1 p
2
p
2
p
2
p
2
p
0
1 qq
0
1
i
qq
0
1 q
01
(1 )
qq
01
(1 )
i
qq
1
01
(1 )
K
qq
2
1
01
qq
01
i
qq
Fig. 2 Markov chain of HOL packet for IEEE 802.15.4
1712 Wireless Netw (2013) 19:1709–1724
123









