ANSYS大变形分析教程：弹簧片实例

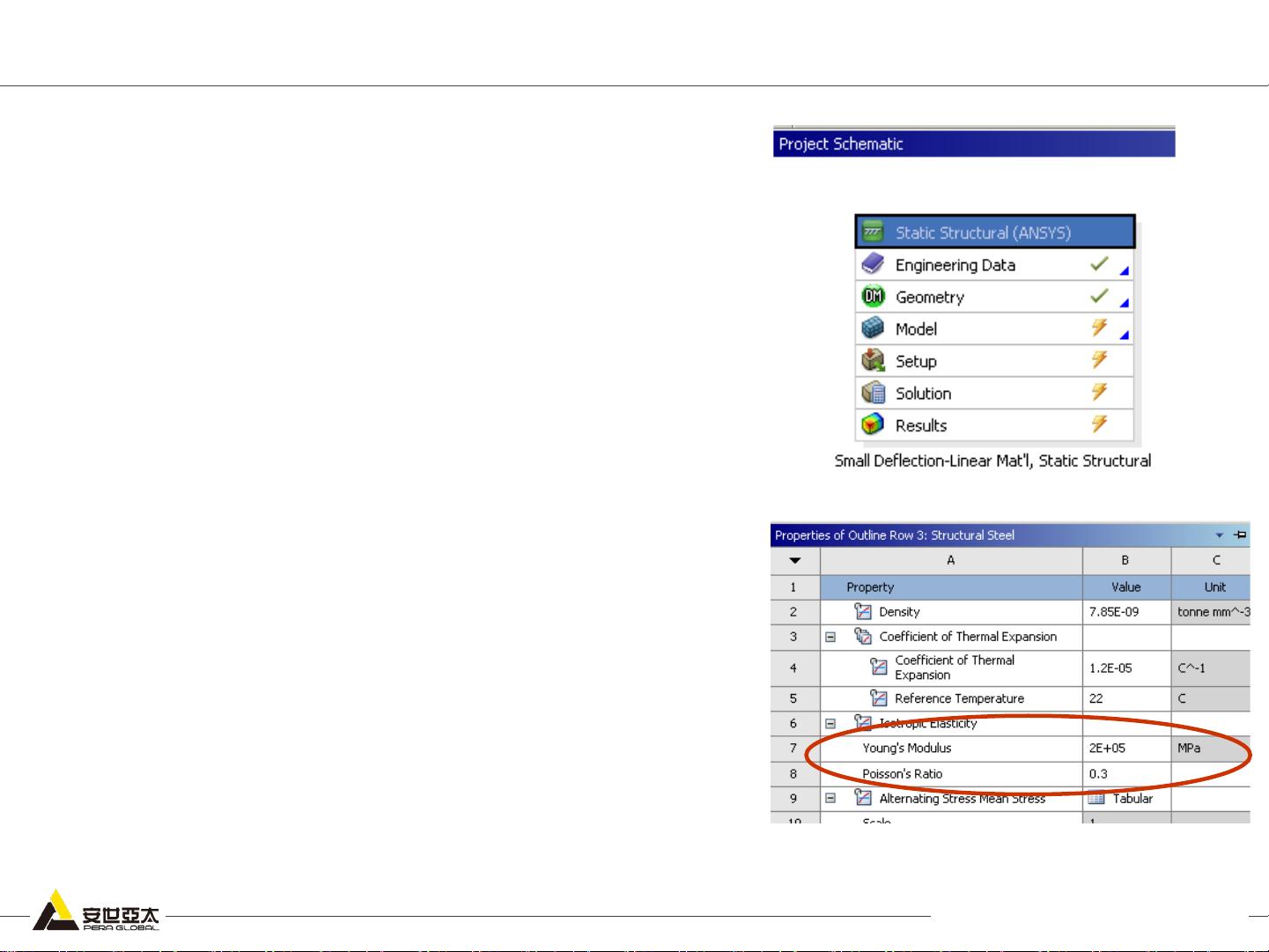
"Mech-SNL_16.0_WS-02A-大变形.pdf" 是一份关于ANSYS有限元分析中大变形处理的教程文档，通过实例对比小变形和大变形分析的区别。 在工程领域，有限元分析（Finite Element Analysis, FEA）是一种常用的技术，用于模拟和预测复杂结构在不同条件下的行为。此文档主要关注的是在ANSYS Workbench环境中进行的大变形分析。大变形分析适用于那些变形程度显著，可能影响到几何非线性的场景，例如弹性体的大幅弯曲或压缩。 文档首先介绍了对比小变形和大变形分析的目标。小变形分析通常假设物体变形后形状仍接近原始形状，可以忽略形状变化对应力和应变的影响。而大变形分析则考虑了形状的显著变化，这对于理解材料的极限性能和稳定性至关重要。 文档中提到的实例是一个3D弹簧片模型，使用线性钢材料，采用实体单元进行网格划分。模型的一端被固定，另一端施加8MPa的压力荷载。这个简单的模型能够清晰地展示小变形和大变形分析之间的差异。 在实际操作中，用户需要启动ANSYS Workbench，打开提供的项目文件“SNLWS2a-spring.wbpz”。在这个项目中，材料数据和几何信息已经预先定义。用户需要在Mechanical模块中进一步构建和运行有限元模型。这包括校正材料属性，确保使用的是公制单位系统，并检查工作单位是否设置为“Metric(mm,kg,N,s,mV,mA)”。 在Mechanical Session中，用户应确认模型已经正确约束（固支）和加载（压力荷载），以便进行求解。这个过程包括高亮显示约束和载荷，确保它们按照预期设置，以进行有效的分析。 通过这个实例，读者将学习如何在ANSYS中处理大变形问题，理解在不同变形程度下结构响应的变化，这对于设计和优化工程组件，尤其是在承受极端条件的部件，是非常有价值的。大变形分析能够提供更准确的结果，帮助工程师预测材料在极端情况下的行为，避免潜在的设计缺陷。