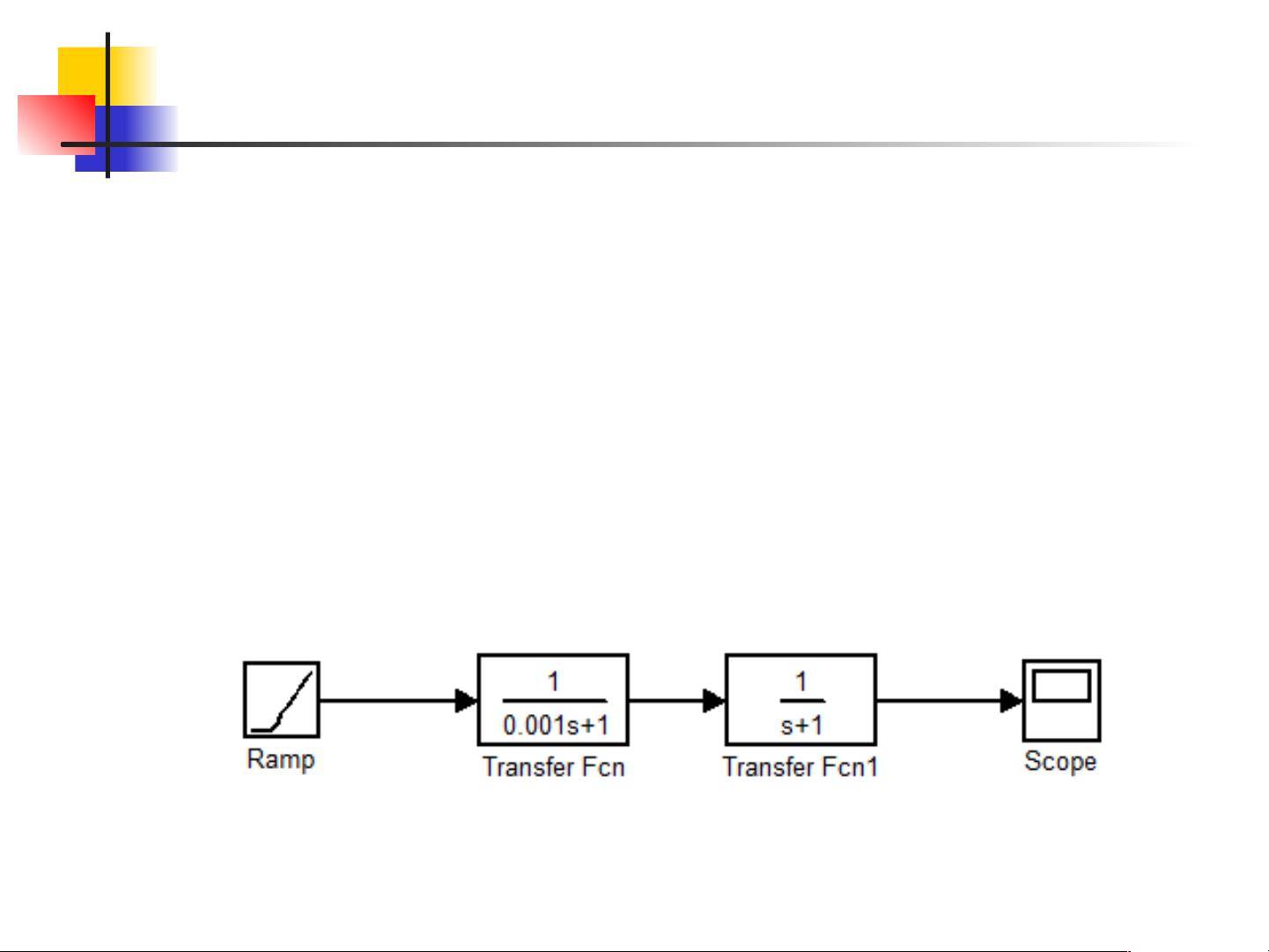
车辆性能仿真：离散化与数值解法详解

本资源是关于车辆性能数字仿真的课程讲义，专精于微分方程数值解法的应用。第三章详尽探讨了数值积分法的基础原理和实际应用，其中包括： 1. **数值积分法基础**：将连续的微分方程离散化，通过设定步长hn，将问题转化为在离散点上求解数值解。稳定性与准确性是选择数值积分方法的重要原则，需满足绝对误差和相对误差准则。 2. **欧拉算法和改进欧拉算法**：这两种算法属于单步显式方法，欧拉算法是最简单的数值积分方法，而改进欧拉算法在一定程度上提高了精度。 3. **龙格-库塔算法**：如RK4（四阶龙格-库塔法）和ode45（Dormand-Prince法）等，它们是多步显式算法，能够提供更高的精度，但计算复杂度相对增加。 4. **离散化与差分方程**：连续系统通过差分方程离散化，形成数值解的初始条件和递推关系，这对于常微分方程组求解至关重要。 5. **单步法与多步法的区别**：单步法仅依赖当前时刻的信息，如前向欧拉法（ode1），而多步法则考虑了过去时刻的信息，如Bogacki-Shampine法（ode3）。 6. **显式与隐式算法**：显式算法如RK4仅使用已知数据求解，而隐式算法如ode23包含未知量，需要线性或非线性方程求解。 7. **定步长与变步长积分算法**：定步长算法固定每一步的时间间隔，如ode45，而变步长算法如ode23可根据系统状态动态调整步长，提高精度，但可能不适用于实时仿真。 8. **Matlab和Simulink工具**：这些工具提供了多种数值积分函数，如ode45是Matlab中的默认连续模型求解器，适合于大部分情况，而ode23则可能在某些复杂系统中表现更优。 通过学习这些内容，学生将能掌握如何运用数值积分法有效地模拟和分析车辆性能，包括动力学行为、稳定性分析以及在实时或非实时环境下的仿真优化。理解这些算法的原理和选择合适的算法对于提升车辆性能预测的准确性和效率至关重要。