哈夫曼树与编码：原理、算法及代码实现

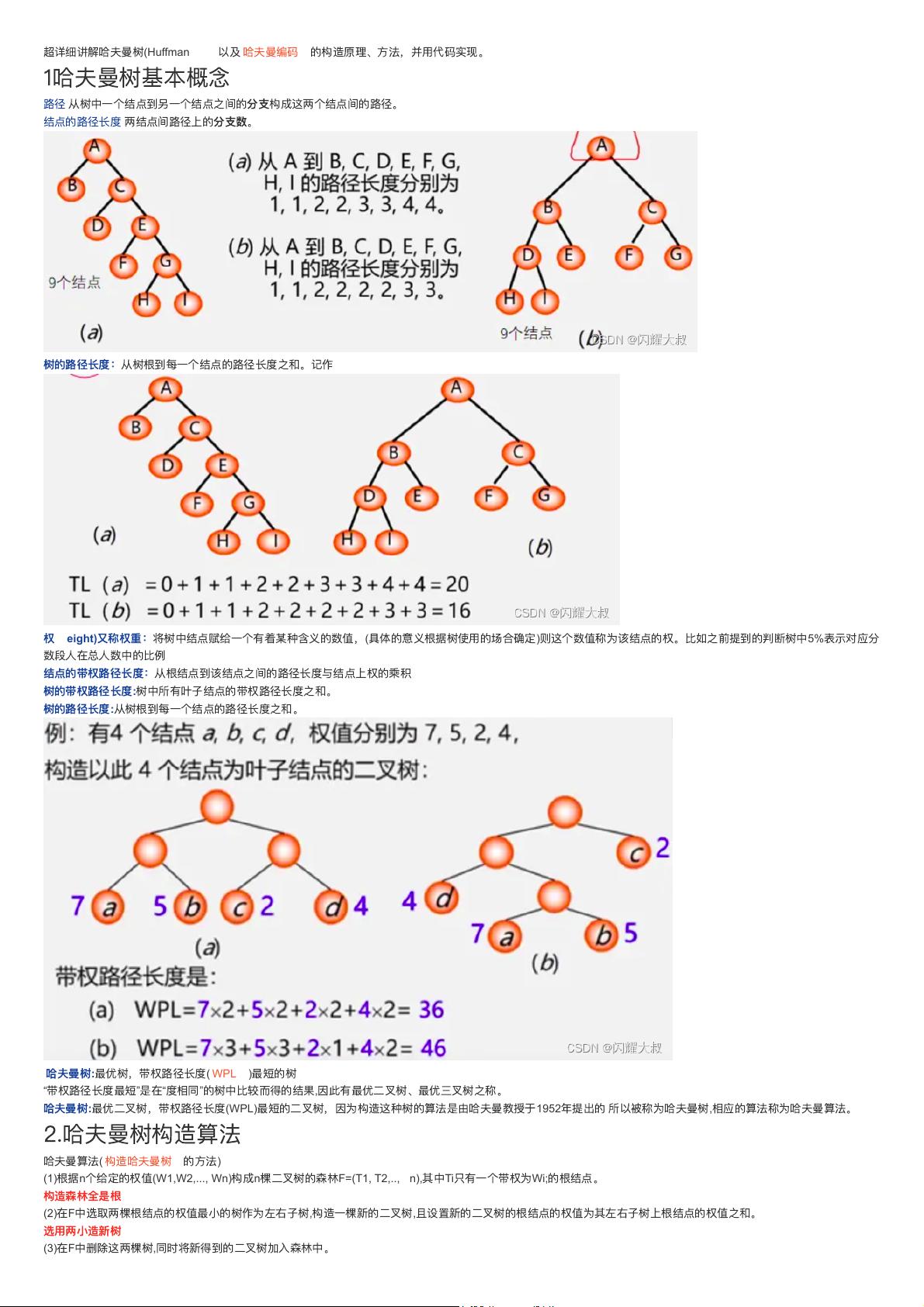
"哈夫曼树(Huffman Tree)与哈夫曼编码是数据结构与算法领域中的重要概念，主要用于数据压缩和编码优化。哈夫曼树是一种特殊的二叉树，也被称为最优二叉树，其特点在于具有最短的带权路径长度。这种树结构在各种应用中，如文本压缩、通信等领域，都能有效地提高效率。 哈夫曼树的基本概念包括以下几个方面： 1. **路径**：在树中，从一个节点到另一个节点之间的分支构成了它们之间的路径。 2. **节点的路径长度**：从一个节点到另一个节点的路径上分支的数量。 3. **树的路径长度**：从树的根节点到所有节点的路径长度之和，记作TL。 4. **权重**（Weight）：在树的上下文中，节点被赋予了具有特定意义的数值，这个数值就是节点的权重，它可以代表不同的含义，如在哈夫曼树中可能代表字符出现的频率。 5. **节点的带权路径长度**：从根节点到节点的路径长度与其权重的乘积。 6. **树的带权路径长度**：树中所有叶子节点的带权路径长度之和，这也是哈夫曼树优化的目标。 哈夫曼树的特性是带权路径长度(WPL)最短，这意味着在具有相同度数的树中，它是最优的。这种特性使得哈夫曼树在数据编码和压缩中特别有效。 哈夫曼树的构造算法通常分为以下步骤： 1. **初始化**：根据给定的n个权重值创建n棵二叉树，每棵树只有一个根节点，其权重值等于对应的给定值。 2. **合并**：每次选择森林中权值最小的两棵树，将它们合并成一棵新树，新树的根节点的权重是这两棵树的根节点权重之和。 3. **迭代**：重复步骤2，直到森林中只剩下一棵树，这棵树就是哈夫曼树。 在构建哈夫曼树的过程中，会进行n-1次合并，产生n-1个新节点，这些新节点都是有两个子节点的内部节点。因此，哈夫曼树共有2n-1个节点，其中所有内部节点的度数都不为1。 为了实现哈夫曼树，我们需要定义节点的数据结构，通常包括节点的值（权重）、左子节点和右子节点的引用。在实际编码中，还会使用队列或堆来辅助构建过程，确保每次都能找到权值最小的节点进行合并。 哈夫曼编码是基于哈夫曼树构建的一种变长编码方式，每个字符或符号都会被分配一个唯一的二进制编码，短编码分配给频率高的字符，长编码分配给频率低的字符。这样，频繁出现的字符在编码后占用的位数较少，从而达到数据压缩的目的。 哈夫曼树和哈夫曼编码是数据压缩技术的核心，通过构建最优的二叉树结构，可以实现高效的数据编码，广泛应用于文件压缩、网络传输等领域。理解和掌握这些概念对于提升算法设计和分析能力至关重要。"