C#实现图算法:数据结构与最短路径解析
130 浏览量
更新于2024-06-29
收藏 619KB PPTX 举报
"解决图的编程问题.pptx - 讲解如何在C#中处理图的编程问题,包括数据结构、图的遍历算法、最小生成树和最短路径等概念,结合高速公路交通网的实例进行说明。"
在计算机科学中,图是一种重要的数据结构,用于表示对象之间的关系。在“解决图的编程问题”这个主题中,我们将深入探讨以下几个关键知识点:
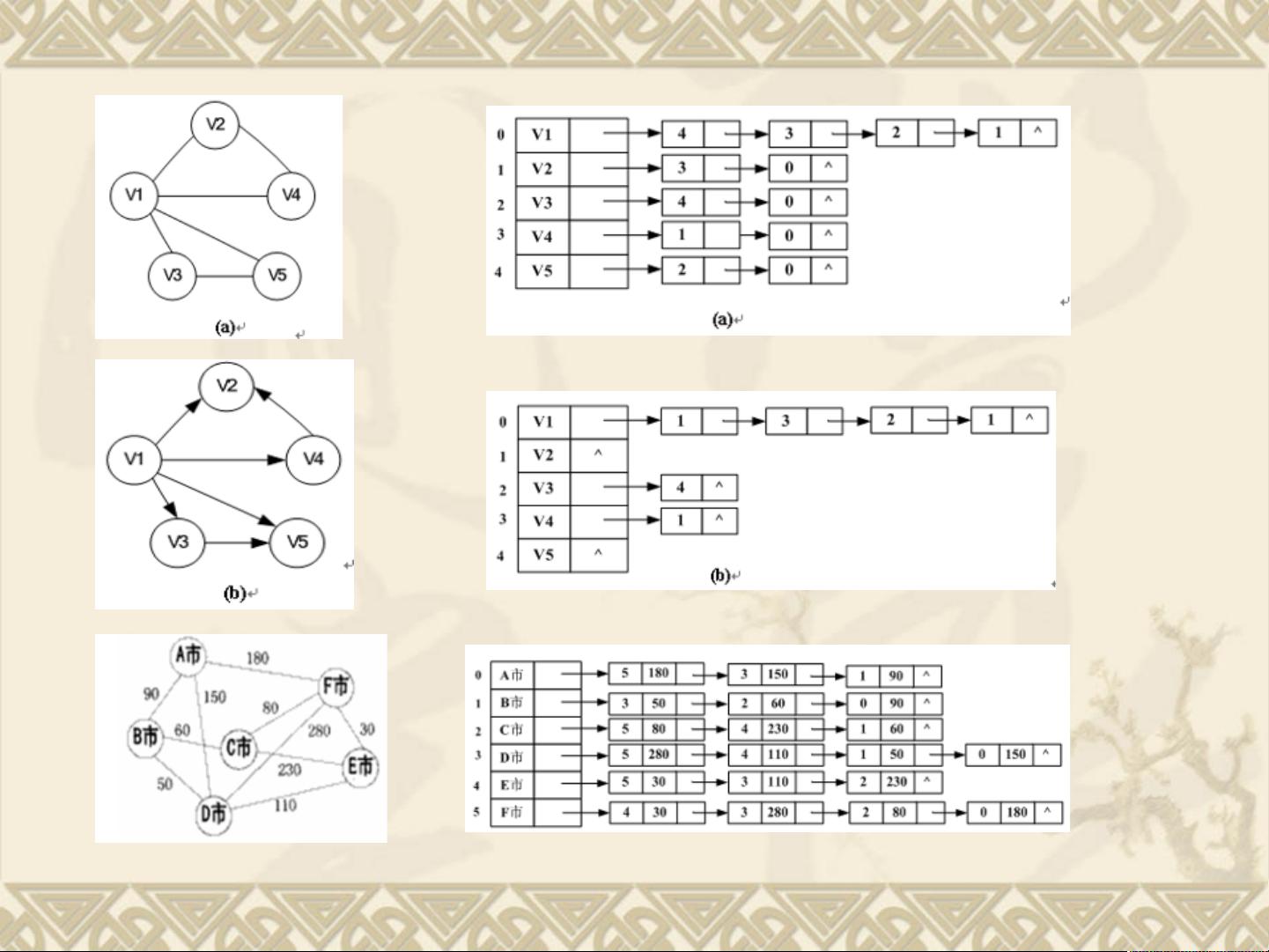
1. **在图中存储数据**:在C#中,图可以使用邻接矩阵或邻接表来表示。邻接矩阵是一个二维数组,每个元素表示两个顶点之间是否存在边;邻接表则更节省空间,它为每个顶点维护一个边的列表,只存储实际存在的边。
2. **图的深度优先搜索(DFS)**:DFS是一种用于遍历或搜索树或图的算法。从一个起始顶点开始,沿着边向下探索,直到到达叶子节点,然后回溯到上一个未访问的节点,继续探索。在C#中,可以通过递归或栈实现DFS。
3. **图的广度优先搜索(BFS)**:BFS从起始顶点开始,逐层探索所有相邻的顶点。使用队列来保持待访问的顶点顺序,确保每次访问最近发现的顶点。BFS在寻找最短路径等问题中非常有用。
4. **最小生成树(MST)**:在加权无向图中,寻找连接所有顶点的边的子集,使得这些边的总权重最小。Kruskal's算法和Prim's算法是两种常见的求解MST的方法,它们都基于贪心策略,但处理边的顺序不同。
5. **图的最短路径**:Dijkstra算法是解决单源最短路径问题的经典算法,适用于加权图。从起点开始,逐步找到到所有其他顶点的最短路径。而Floyd-Warshall算法则可以找出图中任意两点间的最短路径。
6. **实例应用**:高速公路交通网问题展示了图的实际应用场景。每个城市是图中的顶点,城市间的高速公路是边,边上的数字是距离(权重)。程序需要实现存储交通网信息,进行DFS或BFS遍历,以及计算最短路径等功能。
7. **图的术语**:了解图的基本术语,如顶点集、边/弧、度(包括入度和出度)、权等,是理解图论和图算法的基础。有向图和无向图的区别在于边的方向性。
在实际编程中,C#提供了System.Collections.Generic命名空间下的LinkedList和Dictionary等类,可以帮助我们有效地实现图的表示和操作。理解并掌握这些概念和算法对于解决复杂的图问题至关重要,不仅在交通网络规划、社交网络分析、网络路由等领域有广泛的应用,也是算法竞赛和软件开发中的常见工具。
点击了解资源详情
点击了解资源详情
116 浏览量
2022-07-11 上传
2023-12-25 上传
2021-11-14 上传
118 浏览量
136 浏览量
yyyyyyhhh222
- 粉丝: 464
- 资源: 6万+