高级数据结构：平衡二叉树与AVL树解析

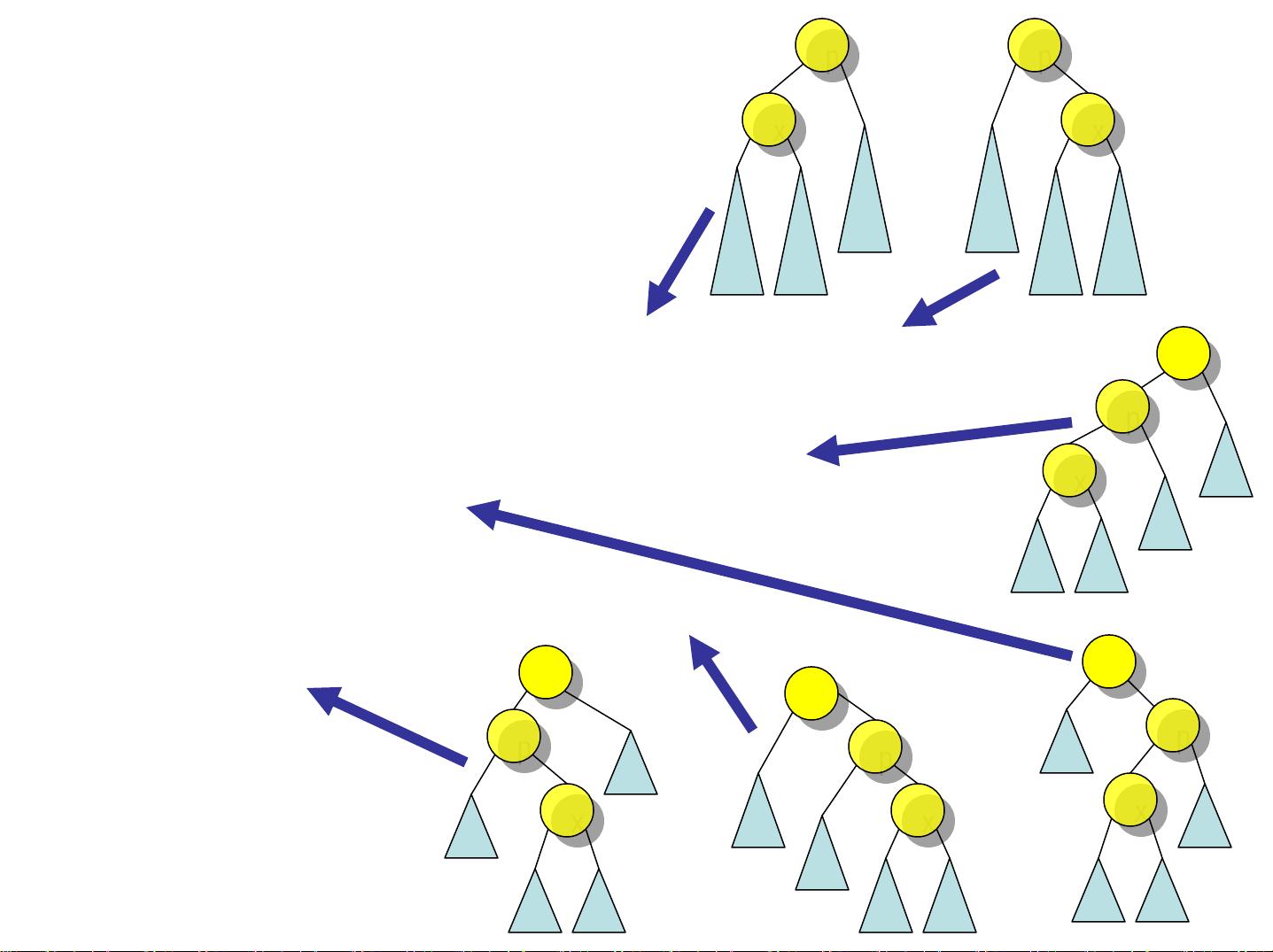
"刘汝佳的高级数据结构课程涵盖了平衡二叉树、可并优先队列、线段树和树状数组基础以及RMQ与LCA等重要概念，适合ACM学习者深入理解数据结构与算法。 一、平衡二叉树 平衡二叉树（Balanced Binary Tree）是一种特殊类型的二叉树，它的左右子树的高度差不超过1，以此确保在操作如查找、插入和删除时能保持高效的性能。基本的二叉搜索树（BST）在极端情况下可能导致高度失衡，例如极度不平衡的树高度可能达到O(n)，这将导致操作效率降低到O(n)。平衡二叉树通过保持树的高度在O(logn)范围内，确保了操作的平均时间复杂度为O(logn)。 二、AVL树 AVL树是最早提出的自平衡二叉搜索树，由G. M. Adelson-Velsky和E. M. Landis于1962年提出。AVL树的每个节点的左右子树高度差不超过1，确保了树的平衡。AVL树的插入和删除操作可能会破坏原有的平衡状态，此时需要通过旋转来恢复平衡。AVL树的旋转分为单旋转和双旋转： 1. 单旋转：当某个子树过高时，以过高子树的父节点为轴进行旋转。分为右旋和左旋。 2. 双旋转：在某些情况下，单旋转无法完全恢复平衡，这时需要对父节点和其子节点进行两次旋转，即先左旋再右旋或先右旋再左旋。 插入算法在AVL树中，从插入的元素开始向上遍历，找到第一个不平衡的节点x，然后根据不平衡情况选择适当的旋转操作来重新平衡树。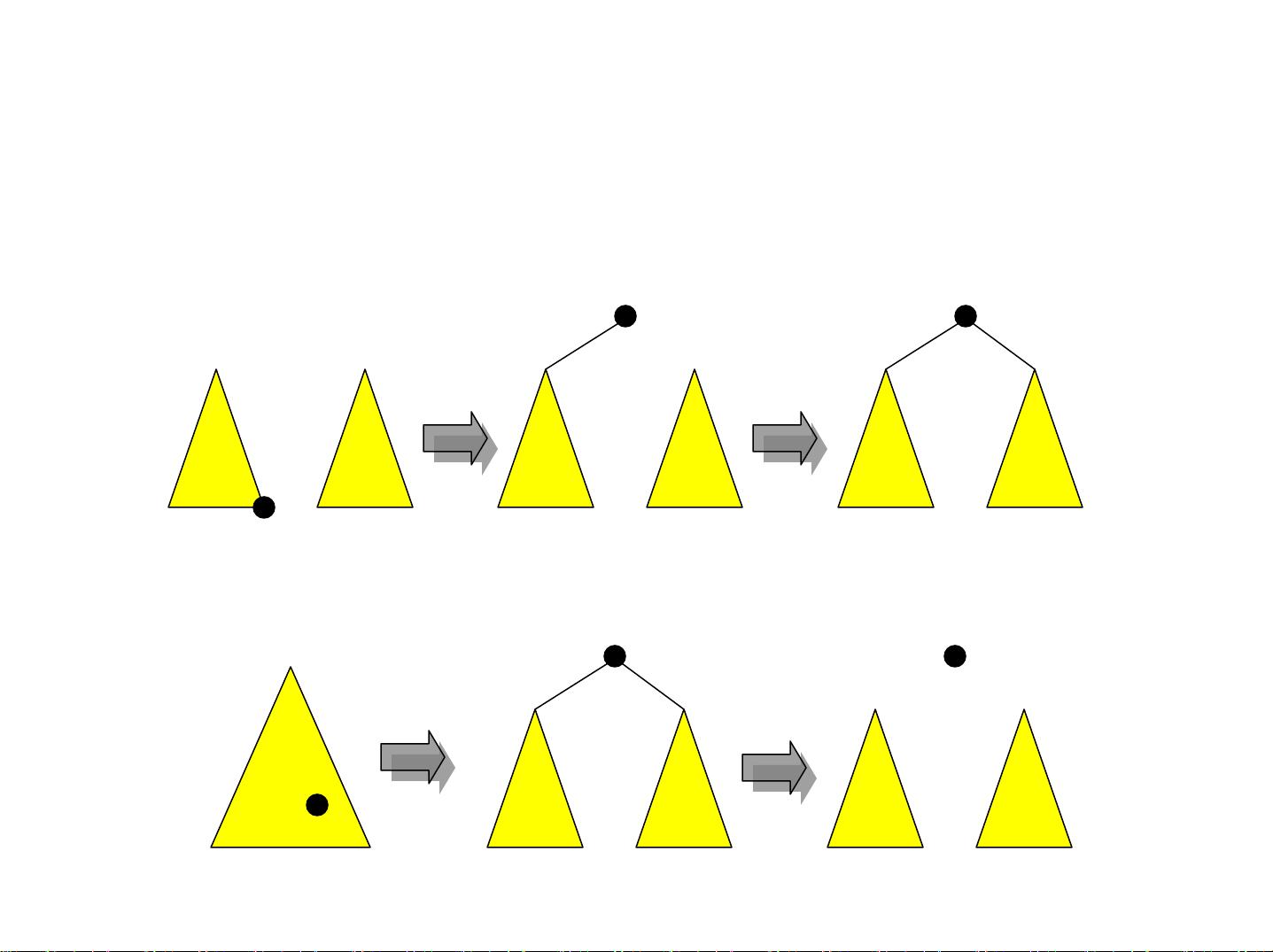 三、可并优先队列（Mergeable Priority Queue） 可并优先队列是一种支持合并和优先级操作的数据结构，常用于求解动态规划问题。它允许高效地合并两个优先队列，同时支持插入和删除最小元素等操作。这种数据结构在处理大量小规模问题时非常有效，如Disjoint Set Union问题。 四、线段树和树状数组 线段树（Segment Tree）是一种树形数据结构，用于高效地处理区间查询和更新操作。它可以用来解决范围查询、区间最大值/最小值等问题。树状数组（Binary Indexed Tree, BIT）则是另一种处理区间问题的高效数据结构，它基于数组，通过前缀和的计算实现区间查询和修改。 五、RMQ（Range Minimum Query）与LCA（Lowest Common Ancestor） RMQ是寻找一个区间内最小值的问题，常见于数组或序列的查询。LCA是图论中的概念，指的是给定图中两个节点的最近公共祖先。在树上高效地计算LCA对于路径查找、最短路径等问题非常重要。 这些高级数据结构和算法在解决复杂问题时具有重要作用，尤其在ACM竞赛和实际编程中，理解和掌握它们能显著提高解决问题的能力和效率。"