探索数字信号处理：离散傅里叶变换DFT详解及其应用

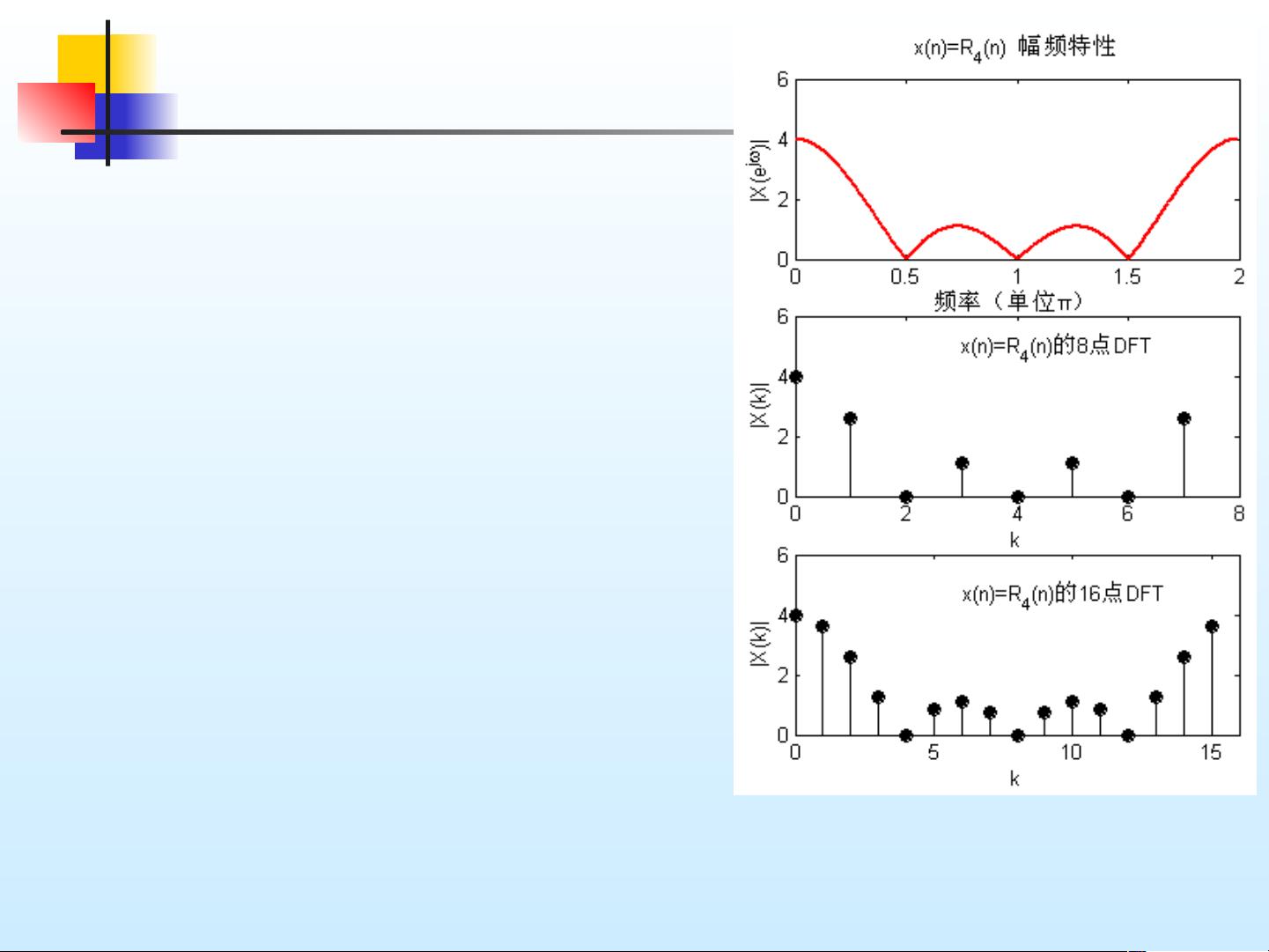
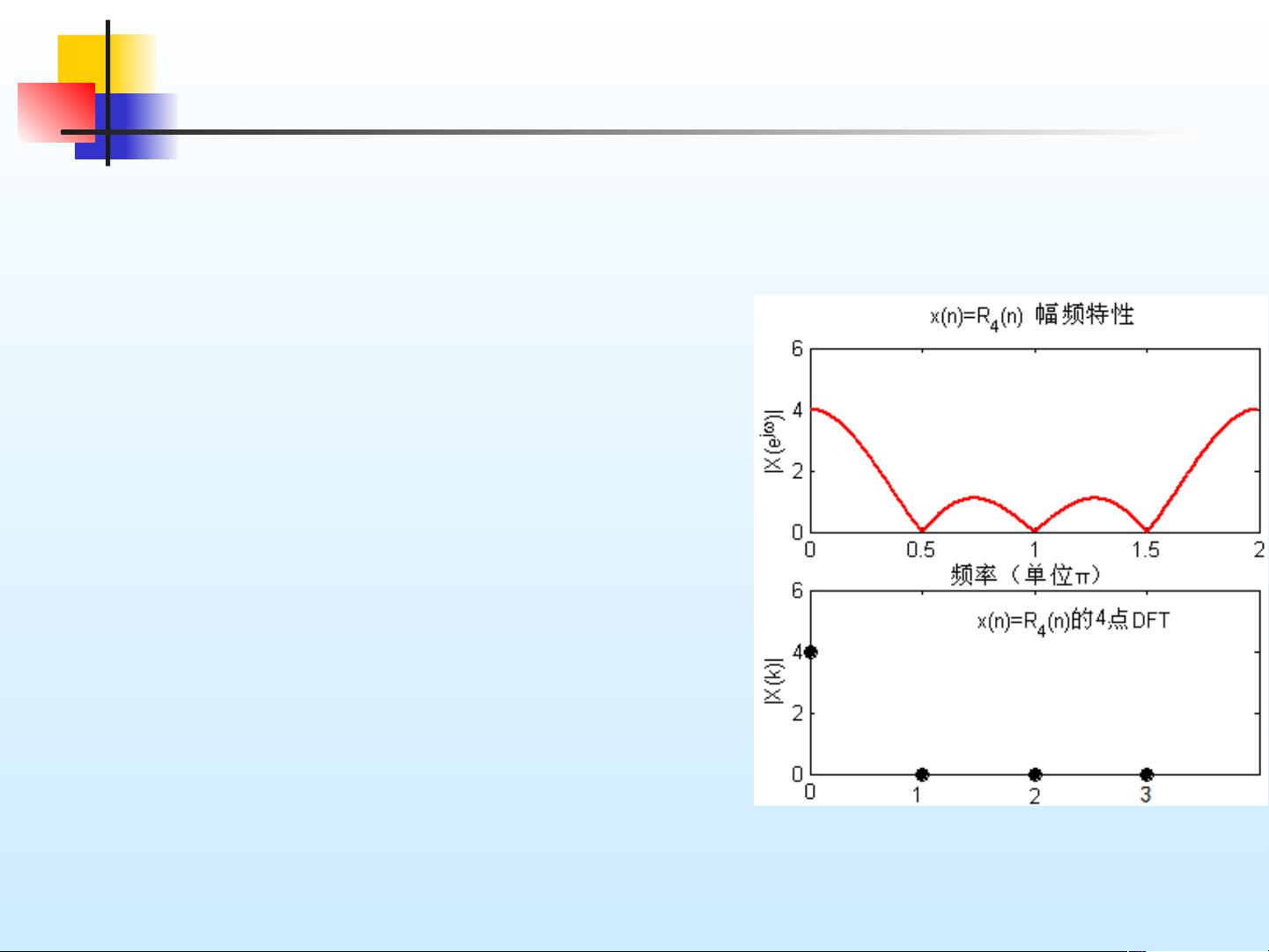
本课件主要涉及的是数字信号处理领域中的重要概念——离散傅里叶变换(DFT)。DFT是信号处理中的基石，它解决了频域离散化的问题，对于信号理论具有深远意义。该章节详细讲解了以下几个关键知识点： 1. **离散傅里叶变换的定义**：对于一个长度为M的有限序列x(n)，定义N点（N通常大于M）的DFT是通过对序列进行周期延拓，然后在单位圆上取N等间距点的复数乘积，最终得到的结果表示为\( X_k = \sum_{n=0}^{N-1} x(n)e^{-j2\pi kn/N} \)。其中，\( N \)是变换区间的长度，\( e^{-j2\pi kn/N} \)是旋转因子。 2. **DFT的性质**：DFT具有线性、周期性和共轭对称性。线性性质表明DFT是对加权和的操作；周期性表示当N增大时，某些频率成分会重复出现；共轭对称性意味着实序列的DFT在负频率部分是实部，正频率部分是虚部的共轭。 3. **频率域采样**：DFT使得频域分析成为可能，通过对信号在频域进行采样，可以了解信号的频率成分分布，这对于信号分析和滤波具有重要作用。 4. **DFT的应用**：DFT的快速算法，如快速傅里叶变换(FFT)，极大地提高了计算效率，使得在实时信号处理中进行谱分析、卷积运算和相关运算变得可行。在计算机上实现这些操作，对通信、图像处理、音频处理等领域至关重要。 5. **DFT与Z变换和傅立叶变换的关系**：DFT可以看作是Z变换在单位圆上的等间隔采样，而傅立叶变换则是连续信号的频域表示，DFT则对应于离散信号的频域采样版。通过对比两者，可以看出DFT是傅立叶变换在离散时间下的具体形式。 理解并掌握离散傅里叶变换是数字信号处理中的基础，它不仅涉及到理论知识，还在实际工程应用中扮演着核心角色。通过深入学习这些内容，能够有效地解析和处理复杂的数字信号，提升信号处理技术的水平。