分形之美：探索摇曳递归分形树与算法设计

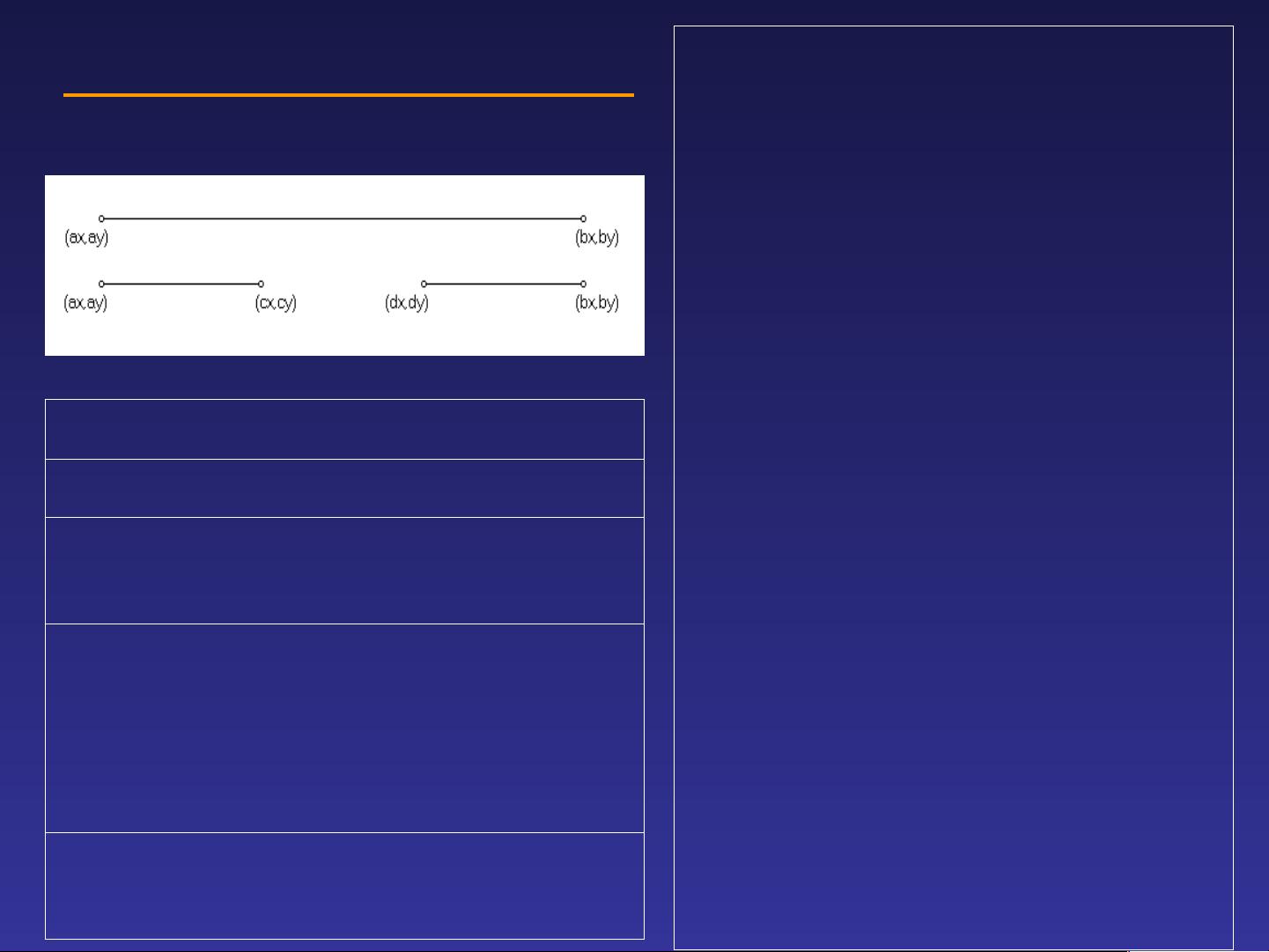
"摇曳的递归分形树-分形算法与程序设计" 这篇内容主要探讨了分形算法和其在计算机图形学中的应用，特别是通过一个名为"摇曳的递归分形树"的例子来展示递归分形的概念。分形是一种几何形状，具有不规则性、自相似性和精细结构的特性。这些特性使得分形在自然界中广泛存在，如树枝、海岸线等。 首先，我们来看分形的含义。"Fractal"一词由数学家曼德勃罗创造，用来描述那些传统几何无法精确描述的复杂无规几何对象。分形的核心特点之一是自相似性，即局部与整体在形状上表现出相似性。此外，自仿射性是自相似性的扩展，意味着局部可以通过非均匀的比例变换映射到整体。 接着，我们讨论分形的几何特征。除了自相似性和自仿射性，分形还具有精细结构，即使在极小的尺度上也呈现出复杂的细节。这使得分形在数学和科学中具有独特的地位，因为它们在不同尺度上都能发现相似的模式。 在度量方面，分形的长度、面积或体积等传统度量方式不再适用。例如，科赫曲线在传统意义上表现为无限长度，而在二维面积上却趋近于零，这展示了分形在欧几里得空间中的非传统性质。因此，引入了分形维数，它通常是一个分数，用于更准确地描述分形的复杂性和维度。 分形维数是一个重要的概念，它可以捕捉到分形体的本质属性，即使在传统维度理论中难以定义的分形也能通过分形维数得到定量描述。例如，一个边长为1的正方形，其二维欧氏维度为2，而某些分形可能具有介于1和2之间的维数，这表明它们既不是典型的线也不是平面，而是介于两者之间的几何实体。 在程序设计中，分形算法通过递归方法实现，如同在描述的"drawLeaf"函数中所示，该函数会递归地绘制树叶形状，每个叶子又由更小的叶子组成，这就是分形自相似性的体现。通过调整参数，可以创造出各种复杂的递归分形树图像，展现出分形的美丽和多样性。 总结来说，分形算法和程序设计是将数学理论应用于艺术和科学的领域，提供了一种理解和表示自然界复杂结构的新视角。通过递归方法，我们可以创建出极具视觉吸引力的图像，并深入了解分形的几何和度量特性。