并行遗传算法在求解函数最大值中的应用

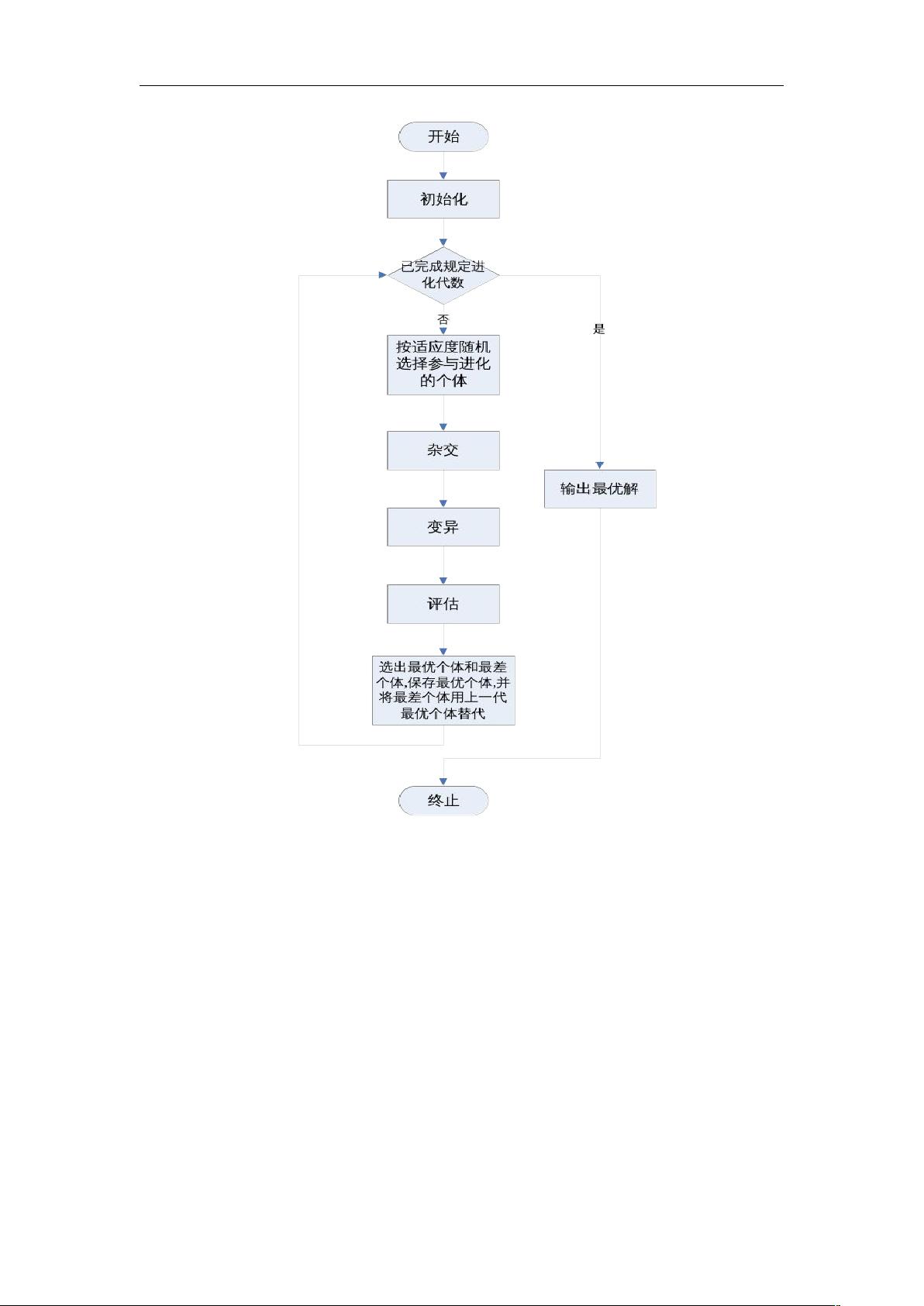
"这篇文档探讨了遗传算法的并行实现，旨在提高计算速度，解决求函数最大值的问题。文中首先介绍了遗传算法的基本概念，强调其基于生物进化论和遗传变异原理，通过群体中的个体和适应度函数进行优化。然后，讨论了串行遗传算法的组成部分，包括染色体表示、适应度函数以及选择机制。适应度函数直接采用目标函数f，选择机制则需平衡适应度好与差的个体存活概率以避免早熟收敛或随机徘徊。最后，文档提出将遗传算法并行化的意图，以解决更复杂的问题，但实际例子中简化为寻找给定函数在定义域内的最大值。" 本文主要知识点如下： 1. **遗传算法基础**：遗传算法是一种模拟生物进化过程的优化方法，利用群体中的个体（染色体）和适应度函数来评估解的质量。适应度好的个体有更高的概率被选中参与下一代的生成。 2. **染色体与适应度函数**：在函数优化问题中，个体的染色体通常由问题的参数构成，如文中提到的n元实数数组。适应度函数直接用目标函数f，即个体对应点在函数f下的值，来衡量个体的优劣。 3. **选择机制**：选择是遗传算法的关键步骤，决定了哪些个体将进入下一次迭代。过度依赖适应度可能导致局部最优，而过于随机则可能使算法失去方向。文中提到的选择机制未具体描述，但提到了需要平衡适应度和随机性。 4. **并行实现**：遗传算法天然具有并行性，因为群体中的个体操作通常是独立的。并行化可以显著提升计算效率，尤其是在处理大规模问题时。文中计划构建并行遗传算法框架，但实例中简化问题为求给定函数的最大值，以节省时间。 5. **问题实例**：文中使用的简单问题是一个n元函数f在定义域D内的最大值搜索，这有助于理解并行遗传算法在解决此类问题时的工作流程和效率提升。 6. **并行化挑战**：并行化过程中需要考虑如何公平地分配计算任务，保持种群多样性，以及如何有效合并不同计算节点的结果，以确保全局最优解的搜索。 7. **性能分析**：并行化后，需要评估算法的收敛速度、资源利用率和并行效率，以证明并行实现的优越性。 通过深入理解以上知识点，读者可以掌握遗传算法的基本原理，了解其在并行计算环境中的应用，以及优化问题的解决策略。并行遗传算法对于处理大规模、高维度的优化问题具有重要价值，尤其在计算资源有限的情况下，能够有效提高求解速度。