"空间数据分析 第7章：内插点领域范围与插值模型选定- 实用方法总结与案例研究"

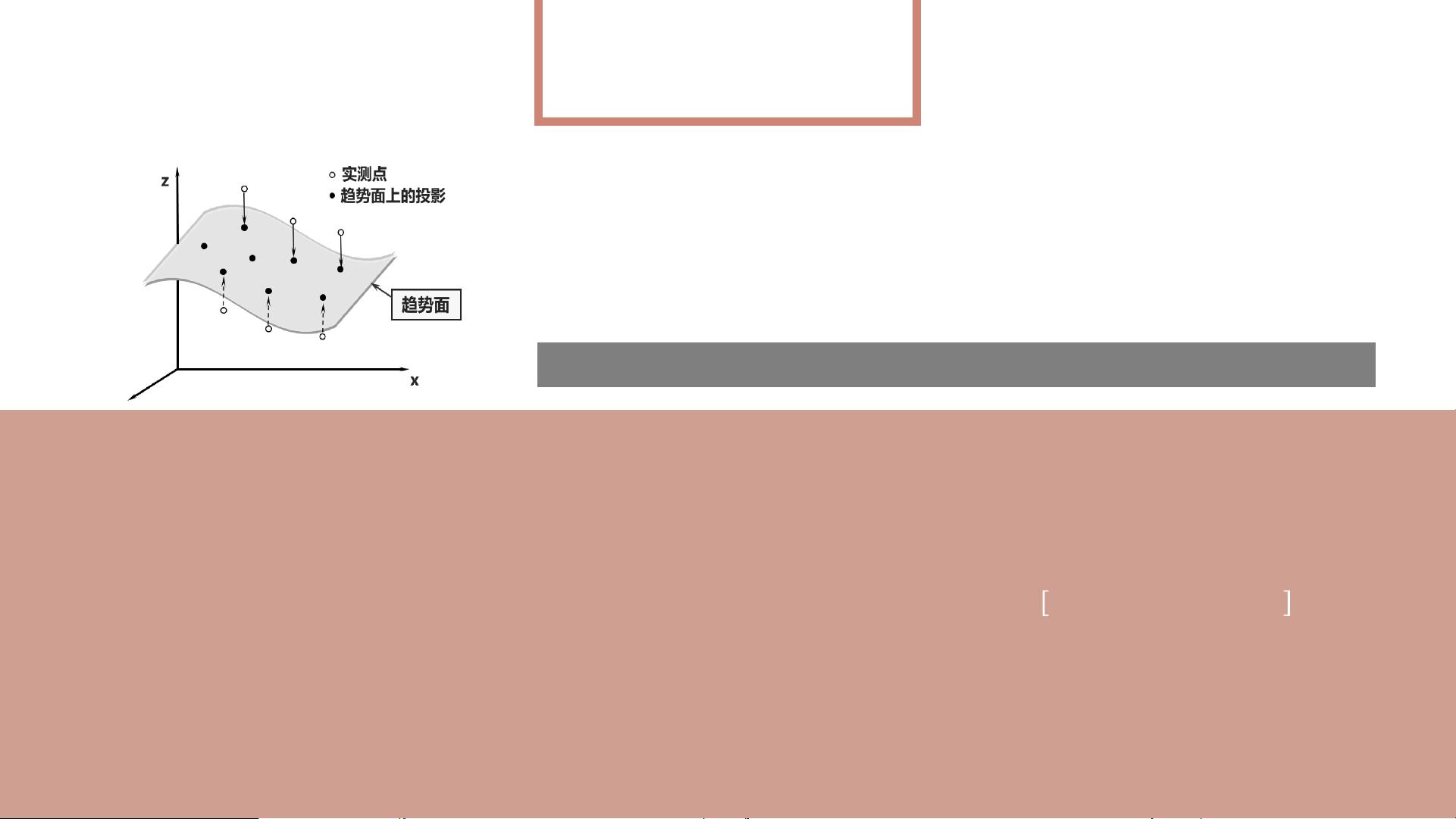
空间数据分析是一项综合性的研究领域，其中空间插值作为其中的重要组成部分，扮演着不可或缺的角色。在第7章中，我们探讨了空间插值的各个方面，从定义内插点领域范围、确定采样点、选定内插数学模型到计算待插点等多个步骤，让我们对空间插值有了更深入的理解。 首先，我们需要定义内插点领域范围，即确定一个覆盖极大和极小值的面积范围内的采样点。这个步骤的重要性在于确保我们能够全面地考虑到数据的变化情况，避免漏掉重要的信息。接着，我们需要确定落入领域内的采样点，这需要对原始数据进行分析和筛选，以确保我们使用的样本具有代表性和可靠性。 在选择内插数学模型的过程中，我们需要考虑是否需要考虑空间权重。空间权重可以帮助我们更好地处理数据之间的空间关系，从而提高插值结果的准确性和可靠性。最后，通过计算待插点，我们可以得到最终的插值结果，从而实现对空间数据的有效分析和预测。 空间插值虽然在一定程度上能够解决数据的空白和不连续性问题，但也存在一些挑战和限制。比如，插值需要密集采样，这会耗费大量的时间、人力和财力。插值结果仍然是以点数据形式存在，对于未采样处的数据仍然未知，仍需要有选择地进行采样，以获取更全面的信息。因此，在实际应用中，我们需要根据具体情况，选取特定的样点进行插值，以获得更准确的结果。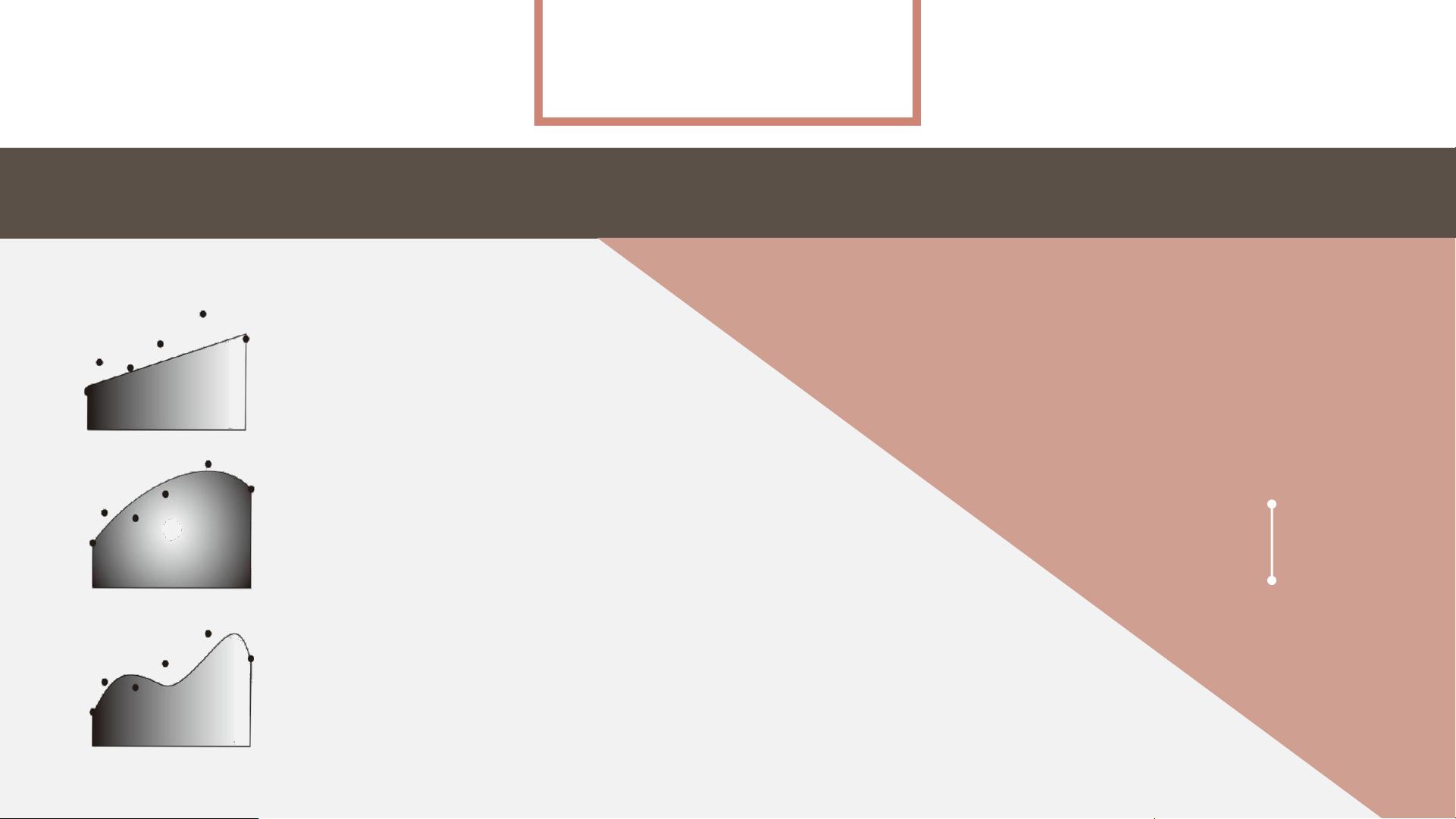 通过空间插值，我们可以得到连续曲面，从而更好地理解已知的空间数据。空间插值分为空间内插法和空间外推法，整体插值和局部插值等不同方法，可以根据实际需求选择合适的插值方法。在具体的插值过程中，常见的方法包括局部多项式插值法、趋势面分析法、克里金插值等，每种方法都有其理论基础和应用范围。 在空间插值中，常见的假设包括变异函数结构、普通克里金法、对数正态克里金法等，这些假设是对数据变异性和空间关系的一种抽象和理论基础。通过这些假设，我们可以更好地理解和处理空间数据，为实际的应用提供支持。 总的来说，空间插值是空间数据分析中的重要方法，通过选择合适的内插点领域范围、采样点、数学模型和计算方法，我们可以实现对空间数据的插值和预测，为决策提供支持和参考。在未来的研究和实践中，我们需要进一步深化对空间插值方法的理解和运用，不断完善和提升空间数据分析的水平和效果。