离散小波变换与多分辨率分析详解

"离散小波变换的多分辨率分析是小波分析中的核心概念，它在80年代末由Mallat和Meyer提出，对于理解离散小波变换及其在计算机上的实现至关重要。多分辨率分析提供了一种信号分解和重构的框架，尤其适用于信号处理和图像分析等领域。本文档介绍了多分辨率分析的基本概念、定义、算法以及其在实际应用中的作用。" 离散小波变换的多分辨率分析是研究离散信号的小波变换的一种方法，它在信号处理和图像分析中扮演着重要角色。这一理论由Mallat提出的算法所驱动，结合了多抽样率信号处理的滤波器组和图像处理中的金字塔编码，使得小波分析变得更加高效和实用。 4.1 多分辨率分析的引入 多分辨率分析主要关注信号的分解近似。通过不同基函数和不同分辨率水平对信号进行近似。例如，使用函数φ(t)及其整数位移作为基，构建正交基。这些基函数在不同分辨率下的投影可以表示信号的近似，提供了一种逐步细化或粗化的信号表示方式。 4.2 多分辨率分析的定义 在多分辨率分析中，信号空间V_j被定义为一系列嵌套的子空间，每个子空间对应不同的分辨率。这些子空间可以用来分解信号，其中较低分辨率的子空间包含较高分辨率子空间的信息。例如，V_0是最基础的空间，而V_j是通过一系列伸缩和平移操作从V_0生成的更高分辨率空间。 4.3 空间V_j和W_j中的信号分解 信号x(t)可以在V_j空间中通过一组基函数进行近似，形成低频部分，而在W_j空间中则包含高频细节。这种分解允许信号在不同尺度上被分析，从而捕捉到信号的局部特征和全局结构。 4.4 二尺度差分方程 二尺度差分方程是多分辨率分析中的关键组件，它描述了如何从一个分辨率级别过渡到下一个级别。这通常涉及到一对共轭正交滤波器，用于下采样和上采样信号，同时保持信息的完整性。 4.5 二尺度差分方程与共轭正交滤波器组 滤波器组由一对滤波器h(t)和g(t)组成，它们满足正交性和完美重构条件。通过这些滤波器，信号可以被分解为低频部分和高频部分，这两部分分别对应于多分辨率分析的V_j和W_j空间。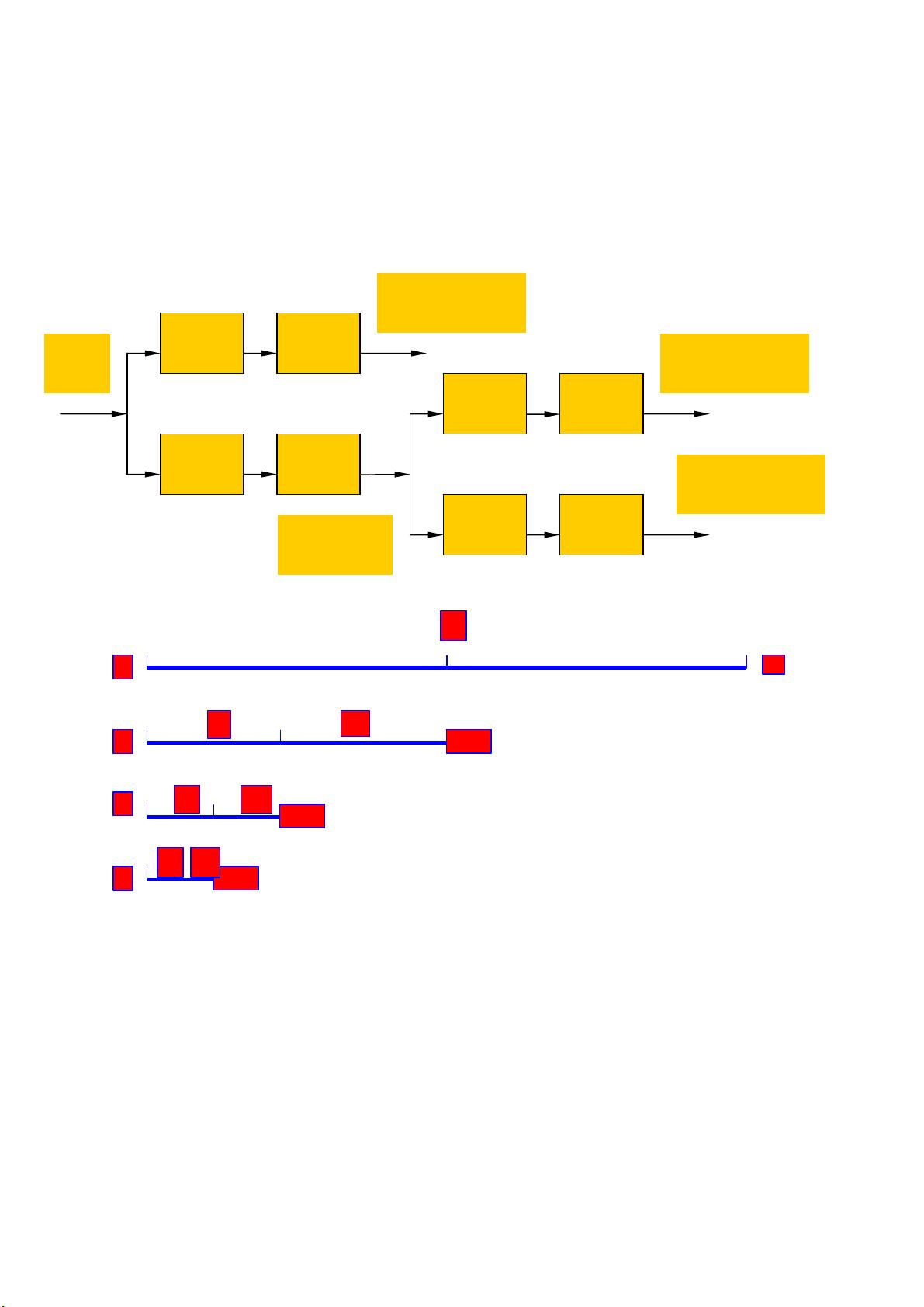 4.6 Mallat算法 Mallat算法是实现离散小波变换的一种快速算法，它利用了二尺度差分方程和滤波器组的概念。通过迭代应用滤波器和下采样过程，信号可以在多个分辨率层次上被分解和重构。 4.7 Mallat算法的实现 在计算机上，Mallat算法通常通过快速傅里叶变换(FFT)实现，因为它提供了高效的计算手段。通过这种方法，可以快速地执行小波变换，并有效地存储和处理变换结果。 4.8 小结 离散小波变换的多分辨率分析不仅提供了对信号进行多层次分析的工具，而且在实际应用中，如图像压缩、噪声去除、信号检测和特征提取等方面都具有广泛的应用。通过理解多分辨率分析，我们可以更好地理解和利用小波变换的优势，解决各种复杂的问题。