1545-5963 (c) 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 10.1109/TCBB.2016.2550430, IEEE/ACM
Transactions on Computational Biology and Bioinformatics
WANG ET AL.: ANALYZING LARGE BIOLOGICAL DATASETS IN BIOINFORMATICS WITH MAXIMAL INFORMATION COEFFICIENT 3
[15-18]. Of these literatures, how to identify the data cor-
relation has posed significant challenges to the academic
and industrial researchers. There have been a wide range
of methods for identifying interesting relationships be-
tween pairs of variables in large data sets in bioinformat-
ics [19], including methods formulated around the axio-
matic framework for measures of dependence [20], other
state-of-the-art measures of dependence, and several
nonparametric estimation techniques that can be used to
score pairs of variables based on the relationship of the
estimated curve. Methods such as splines and regression
estimators [21] tend to be equitable across functional rela-
tionships but they fail to find many simple and important
types of relationships that are not functional. Although
these methods are not intended to provide generality,
most of them are unsuitable for identifying all potentially
interesting relationships in a large scale data set. Similar
methods such as mutual information estimators, maximal
correlation, principal curve, distance correlation, and the
spearman rank correlation coefficient methods are able to
detect broader classes of relationships. However, these
methods are not equitable even in the basic case of func-
tional relationships: They show a strong preference for
some types of functions, even at identical noise levels. For
example, Reshef [6] has established the generality of max-
imal information coefficient (MIC) through proofs, show-
ing its equitability on functional relationships through
simulations, and observe the intuitively equitable behav-
ior on more general associations.
Although researchers have proven MIC is a creditable
approach to detect the relationships between variable
pairs, it still consumes significant time for analyzing large
scale data set due to the complex calculation process.
With respect to the optimization approaches, GPU and
FPGA based approaches are two dominant methodolo-
gies in heterogeneous architecture design paradigms. For
example, RapidMic [22] is a cross-platform tool for the
rapid computation of the maximal information coefficient
based on parallel computing methods. Through parallel
processing, it can effectively analyze the large-scale bio-
logical datasets with a remarkable reduced computing
time. Similarly a simulated annealing and genetic algo-
rithm was developed [23] to facilitate the optimal calcula-
tion of MIC, and the convergence of SG was proved based
on Markov theory. Lopez-Paz et.al [24] introduce the ran-
domized dependence coefficient, which is a measure of
nonlinear dependence between random variables of arbi-
trary dimension. Kinney et. al [25] identify artifacts in the
reported simulation, in particular for the estimates of mu-
tual information when these artifacts are removed. Re-
cently Nature Biotechnology [26] solicits comments from
several practitioners versed in data-intensive biological
research. Their responses not only highlight the appeal of
methods like MIC for biological research, but also raise
some important reservations as to its widespread use and
statistical power. Paninski [27] presents some results on
the nonparametric estimation of entropy and mutual in-
formation. Kraskov et. al [28] present two classes of im-
proved estimators for mutual information, from samples
of random points distributed according to some joint
probability density. To show the effectiveness of MIC in
medical imaging field, Pluim et.al [29] summarize the
MIC based registration of medical images. Reshef et.al [30]
present the MIC calculation with more comprehensive
understanding to show the effectiveness and efficiency.
Similarly, many scientific applications have been opti-
mized by GPU and FPGA accelerators, such as [31], [5]
and [16]. In particular, these approaches consist of a series
of nodes, each of which has both a CPU controller and a
heterogeneous accelerator. All nodes are under the con-
trolling of the scheduler that is responsible for issuing
tasks and balancing workloads, which increase the design
complexity and burden of the software programmers.
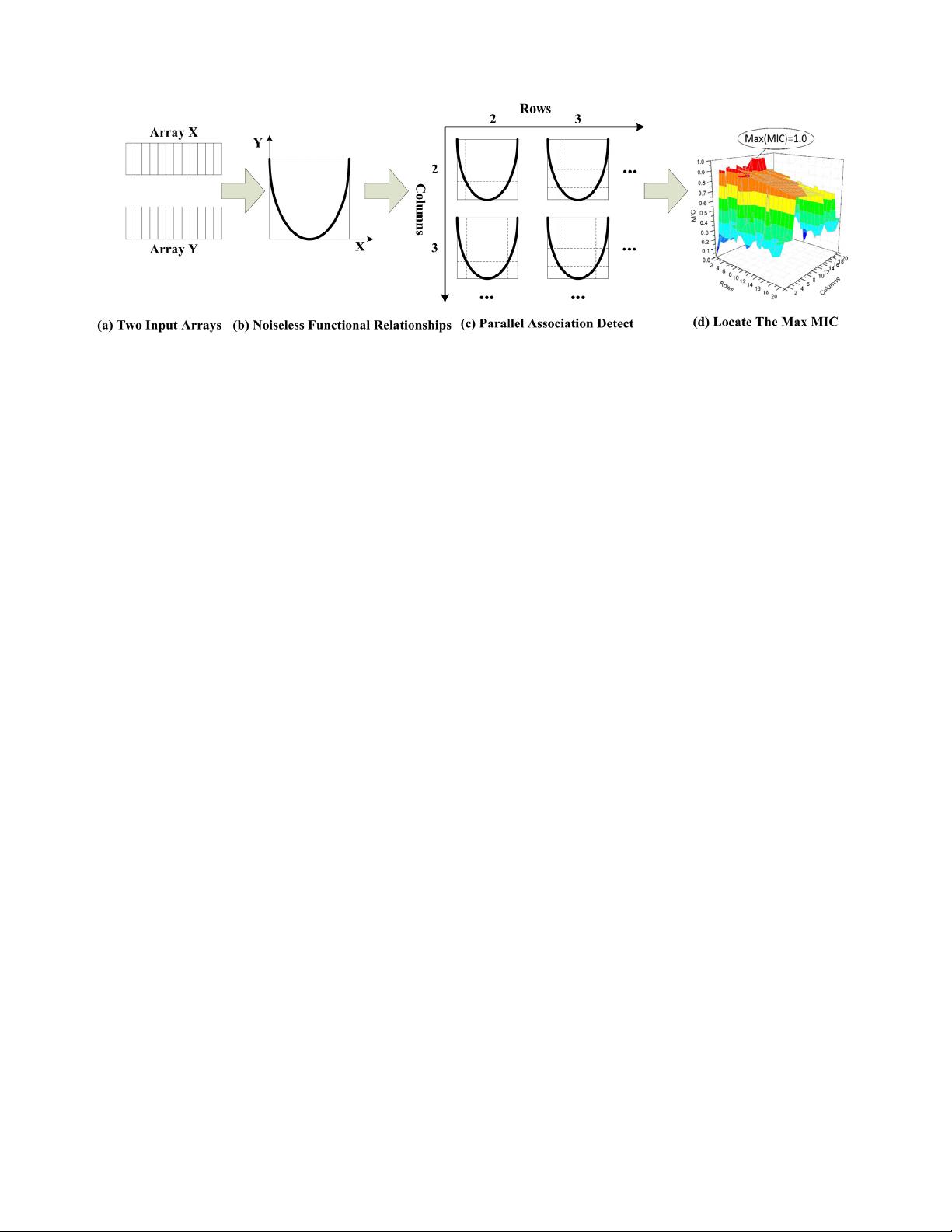
3 MIC CALCULATION ALGORITHM
To reduce the computation complexity in the original
algorithm, Reshef [6] has introduced a dynamic pro-
gramming improvement.
In this section, we will
demonstrate the algorithm first, and then analyze the
strategy of parallelization using MapReduce frame-
work on multiple computing machines
.
3.1. Original Algorithm Description
In particular, the MINE algorithm is designed for heu-
ristically generating the characteristic matrix of two-
variable data sets. To calculate MIC matrix, the algo-
rithm would ideally optimize over all possible grids.
Figure 2. Detailed process of MINE algorithm description









