主成分分析：数据降维与特征提取的关键技术

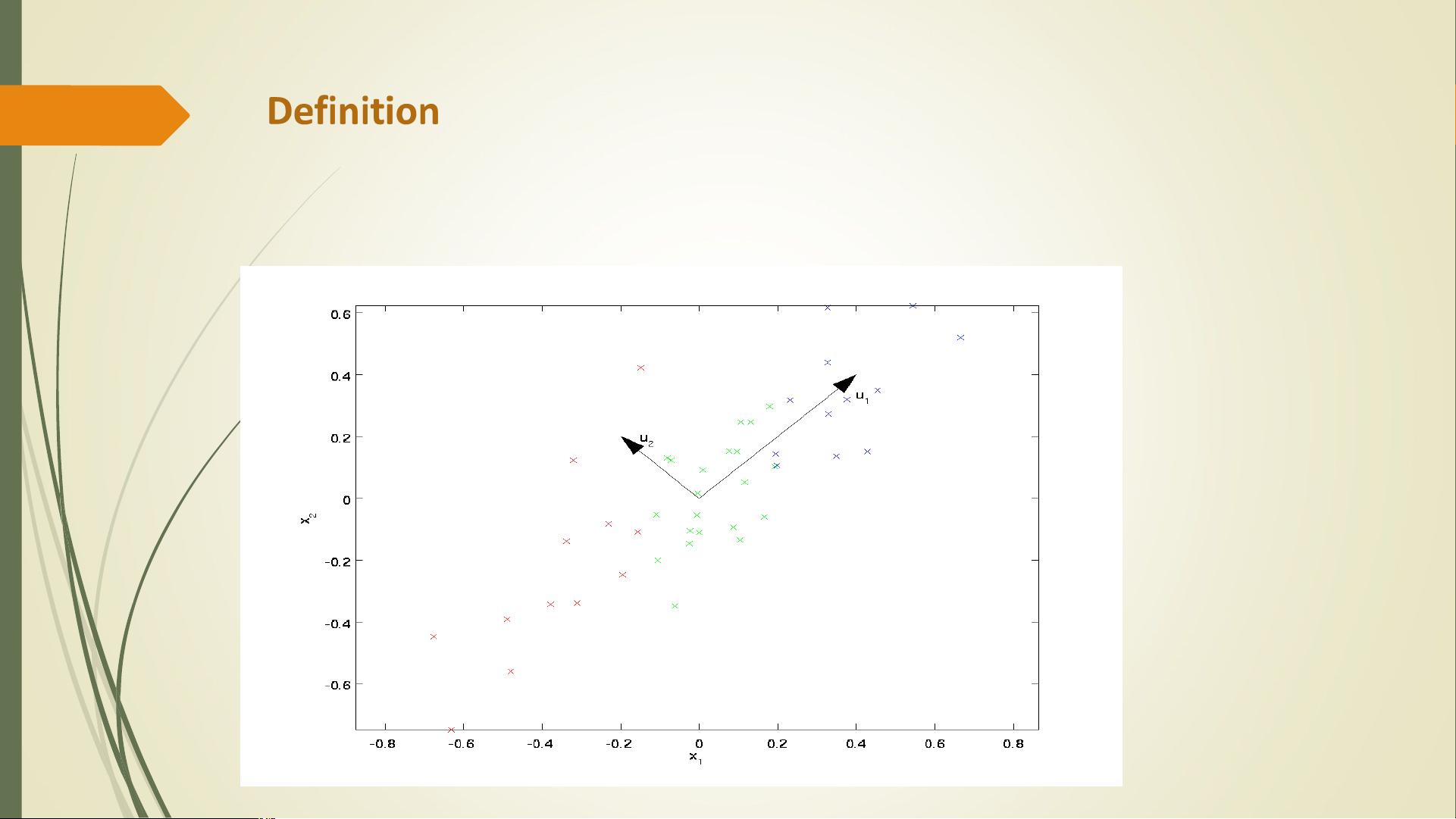
主成分分析（PCA，Principal Components Analysis）是一种常用的数据降维技术，尤其在图像处理和机器学习领域中扮演着关键角色。它通过线性变换，将原始数据从高维空间转换到低维空间，同时尽可能保留数据的主要信息。演讲人喻芳深入解析了PCA的工作原理和应用场景。 PCA的核心思想是通过计算数据集的协方差矩阵，找到一组正交基，即主成分，它们是原始变量线性组合的最佳选择，能最大程度上解释数据的变异性和相关性。这些主成分按其解释数据变异程度的大小排序，第一主成分解释了最多的数据变异，后续的主成分依次递减。 数据预处理是PCA的重要步骤，通常涉及特征标准化。这个过程确保每个特征具有零均值和单位方差，有助于消除量纲效应，使不同的特征在同一尺度上比较。特征标准化的方法包括对每个维度的均值进行减去，然后除以其标准差，这样每个特征的分布就集中在零附近，且方差为1。 计算协方差矩阵是PCA的关键环节，它测量的是不同特征间的变化程度。协方差矩阵的特征向量对应于主成分，特征值则表示主成分的重要性或解释的方差比例。通过计算特征值和特征向量，可以确定数据的主要变化方向和减少维度的数量。 贡献率是对每个主成分解释数据总变异性的百分比，它可以帮助我们决定保留多少主成分以保持足够的信息。通常，我们会选择具有较高贡献率的前几个主成分进行投影，以达到降低维度的目的。 实例计算与分析部分展示了如何具体操作PCA，包括构建标准化矩阵、计算协方差矩阵以及提取主成分的过程。通过这些步骤，我们可以有效地将复杂的数据集转化为低维表示，这对于后续的数据分析、模型训练以及可视化都是非常有益的。 总结来说，PCA是一种强大的数据分析工具，通过标准化、协方差矩阵分析和特征提取，帮助我们理解数据的内在结构，并高效地处理高维数据。理解并掌握PCA的原理和实践方法，对于在各种机器学习项目中优化数据处理流程至关重要。