图灵机与递归可枚举语言：构造与理解

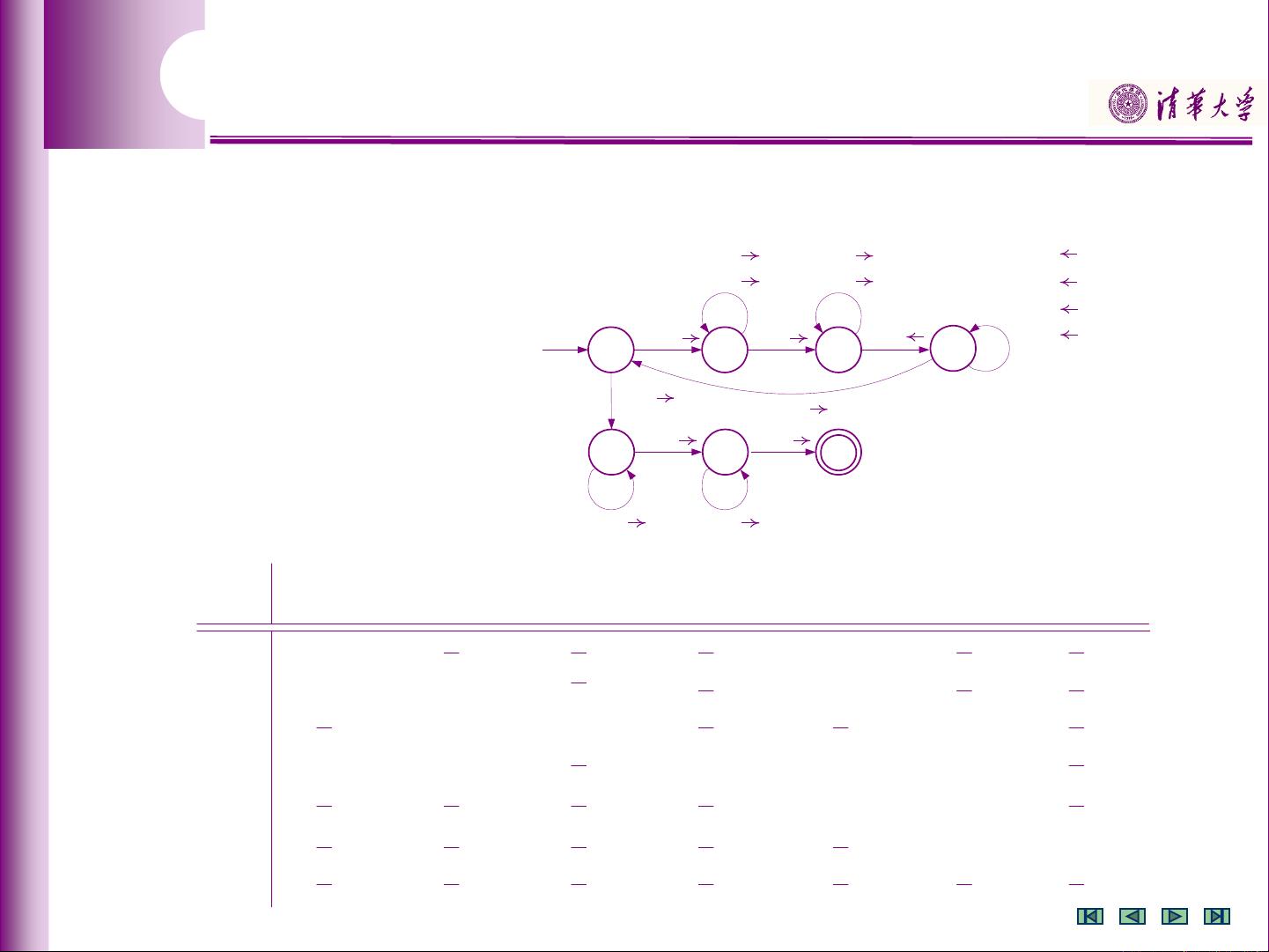
本篇文档是关于形式语言与自动机课程的第十二讲，主要探讨了图灵机（Turing Machine）及其在计算机科学中的核心地位，特别是与递归可枚举语言的关系。首先，我们来概述以下几个关键知识点： 1. **图灵机概念与定义**： 图灵机是一种理论模型，用于模拟计算机执行过程，它由以下组成部分构成： - 有限的状态集（Q，包括起始状态q0） - 输入符号集（，如0,1,2） - 带符号集（，包括空白符B，以及输入符号X,Y,Z等） - 转移函数（），定义状态和带符变化的规则 - 开始状态（q0） - 特殊带符（B，通常表示为空白） - 终态集合（F，表示机器接受或拒绝输入的终结状态，如例中提到的q6） 2. **递归可枚举语言**： 这些语言是能够通过递归算法或图灵机来识别的，它们构成了计算理论上的一类重要语言。在文档中，通过示例说明了一个图灵机能够接受的语言L=0n1n2n...n>1，即所有以0开头，接着是任意多个1和2的序列。 3. **基本图灵机的编程技巧**： 基本图灵机展示了如何设计和理解图灵机的工作原理，包括带的布局、状态转移和符号处理。例如，通过转移函数定义了从一个状态到另一个状态以及改变带上的符号的操作。 4. **图灵机的扩展与限制**： 除了基本图灵机，还有对图灵机进行扩展的概念，如增加内存限制或输入符号，以及受限图灵机，这些都反映了理论上的复杂性和实际应用的局限性。 5. **图灵机与计算机的关系**： 图灵机是理论计算复杂性的基石，尽管现代计算机的设计可能与图灵机模型有所区别，但图灵机的概念对于理解计算机是否能解决所有可计算问题具有重要意义。 在学习这部分内容时，学生需要理解图灵机的基本工作原理，并通过分析递归和非递归语言来加深对计算能力的理解。同时，掌握如何通过图灵机构造和判断特定语言的能力，这对于深入研究算法、编译器设计和理论计算机科学至关重要。