MATLAB中FIR滤波器设计：窗口函数与凯塞窗实例

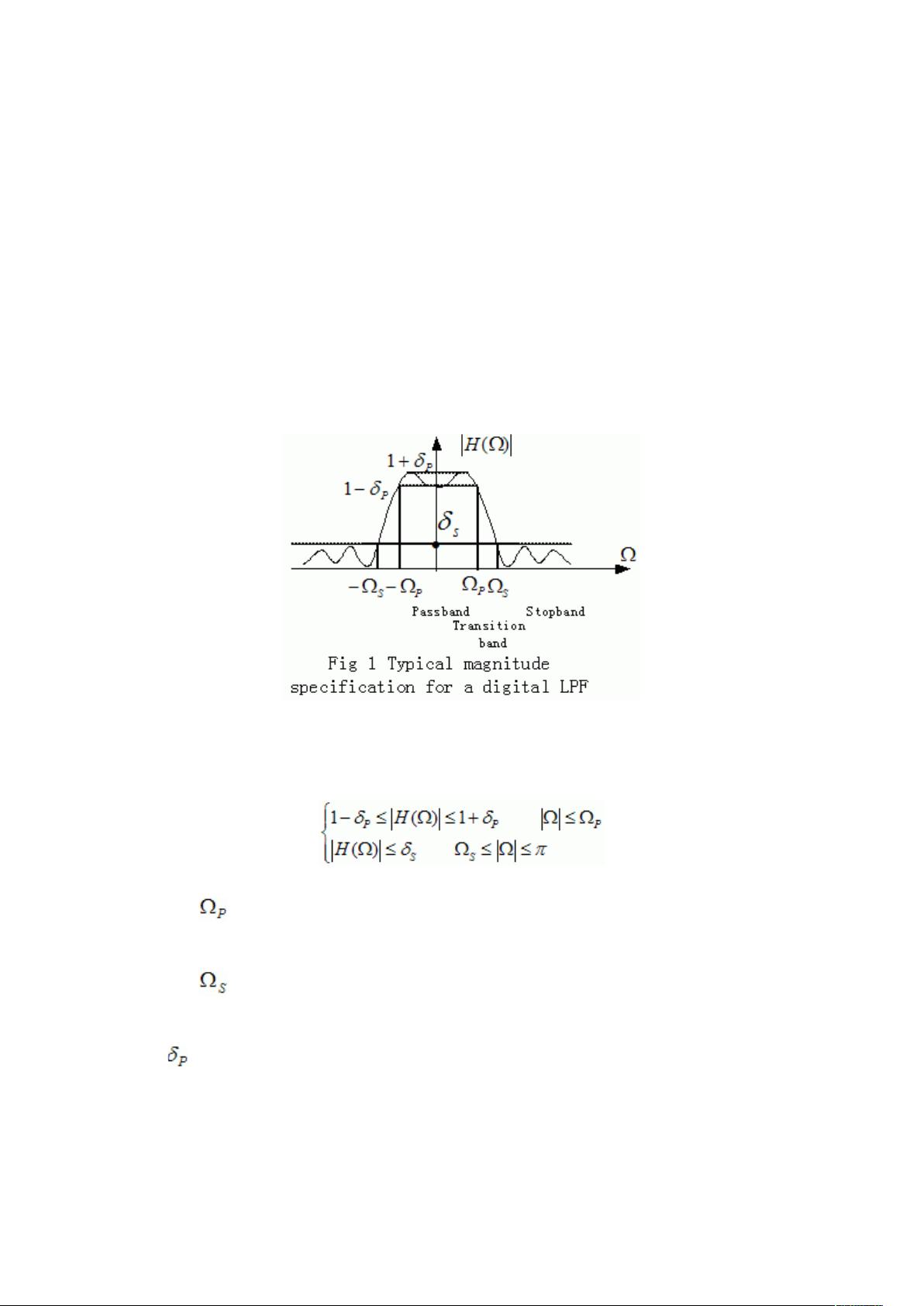
有限冲激响应(FIR)数字滤波器设计是一门重要的信号处理技术，主要应用于信号的滤波、噪声消除和信号特征提取等场景。在这个实验中，其核心目标是加深理解和应用数字滤波器的常见性能指标，并通过MATLAB工具进行滤波器的设计与分析。 实验的目的包括深入理解数字滤波器的关键指标，如通带边缘频率（决定滤波器在信号频谱中允许信号通过的最高频率）、阻带边缘频率（信号被抑制的最低频率）、通带起伏（滤波器在通带内的频率响应变化）、通带峰值起伏和阻带起伏（衡量滤波器陡峭度），以及最小阻带衰减（滤波器在阻带内信号衰减的最低要求）。 MATLAB中的关键函数如`fir1`用于直接设计FIR滤波器，`kaiserord`和`remezord`则用于估计滤波器的阶数和窗口函数参数。`remez`函数则是用于优化窗函数设计，以满足特定的频率响应特性。实验者需要熟练掌握这些函数的使用，以便根据设计要求创建滤波器。 实验的具体内容涉及在MATLAB中运用窗函数法，例如使用凯塞窗口（Kaiser window）设计低通滤波器。通过设定特定的通带和阻带边缘频率以及阻带衰减，`kaiserord`函数计算出所需的滤波器阶数`n`和窗口参数`beta`。然后，使用`fir1`函数结合`kaiser`函数来生成滤波器的系数，进一步通过`freqz`函数计算并绘制滤波器的幅度和相位响应曲线，从而分析滤波器的特性。 在扩展练习中，学生会被要求设计一个具有特定通带和阻带特性的FIR低通滤波器，例如通带边界频率为0.3π和0.75π，阻带边界频率为0.45π，且阻带衰减至少达到50分贝。设计过程中，需通过调整窗口函数参数，如凯塞窗口的长度`N`，来优化滤波器的性能。设计完成后，会展示设计的滤波器频率特性，对比直接截取和凯塞窗设计的结果，以便直观地理解窗口函数对滤波器性能的影响。 有限冲激响应数字滤波器设计实验是一个理论与实践相结合的过程，通过MATLAB工具，学生可以深入理解滤波器设计的基本原理和技巧，同时锻炼编程和信号处理能力。