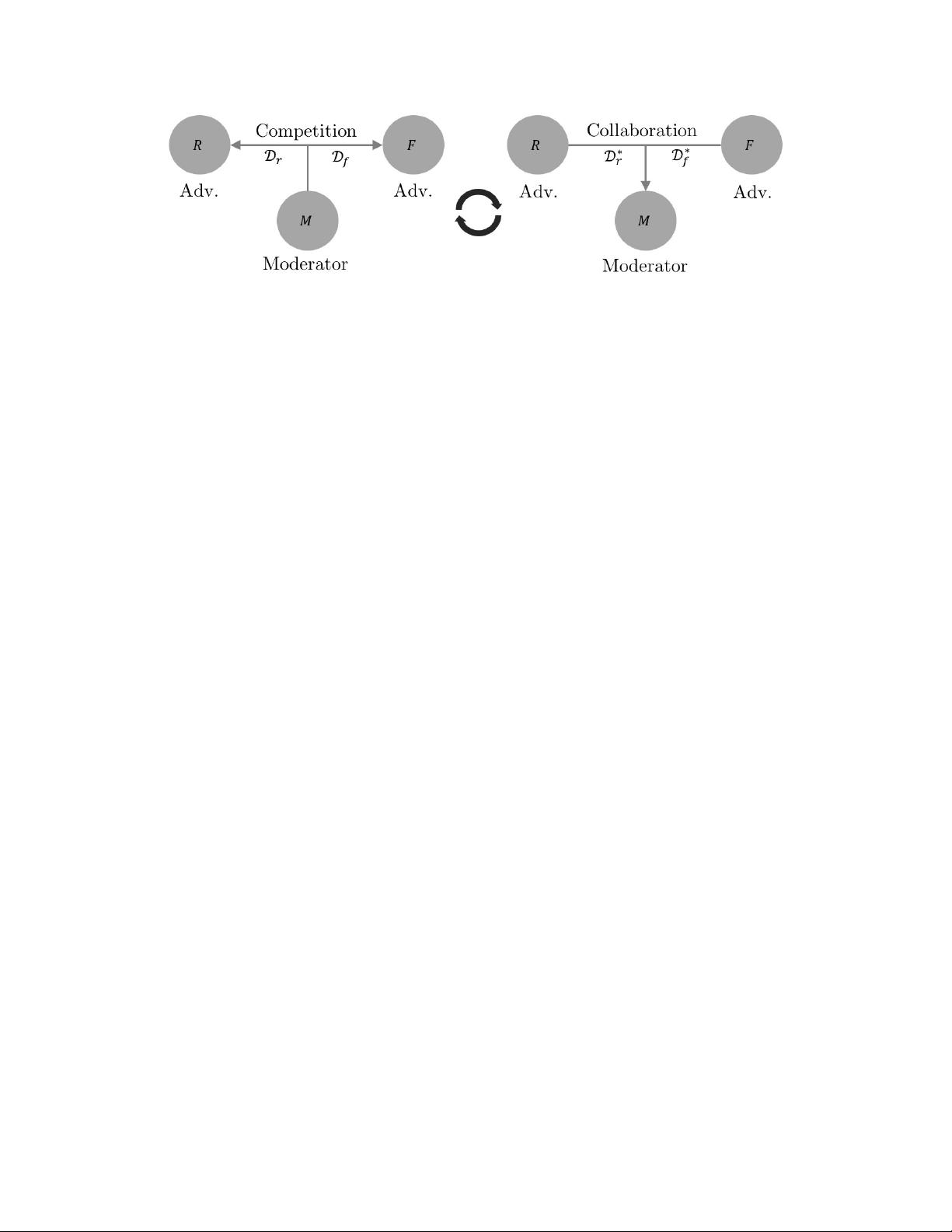
Figure 2: Training cycle of Competitive Collaboration: The moderator
M
drives competition between
two adversaries
{R, F }
(first phase, left). Later, the adversaries collaborate to train the moderator to
ensure fair competition in the next iteration (second phase, right).
In our implementation,
R = (D, C)
denotes the depth and camera motion networks that reason about
the static regions in the scene. The adversary
F
is the optical flow network that reasons about the
moving regions. For training the adversaries, the motion segmentation or mask network
M
selects
networks
(D, C)
on pixels that are static and selects
F
on pixels that belong to moving regions. The
competition ensures that
(D, C)
reasons only about the static parts and prevents any moving pixels
from corrupting its training. Similarly, it prevents any static pixels to appear in the training loss of
F
,
thereby improving its performance in the moving regions. In the second phase of the training cycle,
the adversaries
(D, C)
and
F
now collaborate to reason about static scene and moving regions by
forming a consensus which is used as a loss for training the moderator,
M
. In the rest of the section,
we formulate the joint unsupervised estimation of depth, camera motion, optical flow and motion
segmentation under this framework.
Notation.
We use
{D
θ
, C
φ
, F
ψ
, M
χ
}
, to denote the networks that estimate depth, camera motion,
optical flow and motion segmentation respectively. The subscripts
{θ, φ, ψ, χ}
are the network
parameters. We will omit the subscripts at several places for brevity. Consider an image sequence
I
−
, I, I
+
with target frame
I
, and neighboring reference frames
I
−
, I
+
. In general, we can have
many neighboring frames. In our implementation, we use 5 frame sequences for
C
φ
and
M
χ
. For
simplicity, we use 3 frames to describe our approach. We estimate depth of the target frame as
d = D
θ
(I). (1)
We estimate the camera-motion,
e
of each of the reference frames
I
−
, I
+
w.r.t the target frame
I
as
e
−
, e
+
= C
φ
(I
−
, I, I
+
). (2)
Similarly, we estimate the regions that segment the target image into static scene and moving regions.
The optical flow of the static scene is a result of only the camera motion. This generally refers to
the structure of the scene. The moving regions have independent motion w.r.t to the scene. The
segmentation masks corresponding to each pair of target and reference image are given by
m
+
, m
−
= M
χ
(I
−
, I, I
+
), (3)
where
m
+
, m
−
∈ [0, 1]
are the probability of regions being static. Finally, the network
F
ψ
estimates
the optical flow for the moving regions in the scene.
F
ψ
works with
2
images at a time, and its
weights are shared while estimating u
−
, u
+
, the backward and forward optical flow respectively.
u
−
= F
ψ
(I, I
−
), u
+
= F
ψ
(I, I
+
). (4)
Loss.
We learn the parameters of the networks
{D
θ
, C
φ
, F
ψ
, M
χ
}
by jointly minimizing the energy
E = λ
R
E
R
+ λ
F
E
F
+ λ
M
E
M
+ λ
C
E
C
+ λ
S
E
S
, (5)
where
{λ
R
, λ
F
, λ
M
, λ
C
, λ
S
}
are the weights on the respective energy term. The terms
E
R
, E
F
are
the objectives that are minimized by the two adversaries reconstructing static and moving regions
respectively. The competition for data is driven by
E
M
. A larger weight
λ
M
drives more pixels
towards static scene reconstructor. The term
E
C
drives the collaboration and
E
S
is a smoothness
regularizer. Ergo, E
R
minimizes the photometric loss on the static scene pixels given by
E
R
=
X
Ω
ρ
I, w
c
(I
+
, e
+
, d)
· m
+
+ ρ
I, w
c
(I
−
, e
−
, d)
· m
−
(6)
4









