掌握工学初学者传递函数：概念、推导与应用

传递函数是工学领域中分析线性控制系统动态特性的核心工具，尤其对于初学者来说，理解和掌握这个概念至关重要。传递函数的基本概念包括以下几个方面： 1. **定义**： - 当一个线性控制系统接受输入信号r(t)，输出信号c(t)，并且假设初始条件为零时，输出c(t)的拉氏变换C(s)与输入r(t)的拉氏变换R(s)的比值，称为系统的传递函数。其数学表达为C(s) = (s)/[B(s)A(s)]，其中B(s)和A(s)分别是系统的开环增益和开环传递函数。 2. **性质**： - **对应性**：传递函数是系统动态行为的数学模型，它与系统的微分方程有着直接的对应关系，通过传递函数可以直接了解系统的响应特性。 - **系统特性**：传递函数反映了系统的固有特性，即系统对于不同输入信号的响应只取决于传递函数的形式和参数，而不受具体输入信号的影响。 - **形式**：传递函数通常表现为复变量s的有理真分式，分母多项式的阶数n应大于或等于分子多项式的阶数m，即n >= m。 - **系数**：传递函数的系数都是实数，这使得传递函数具有直观的物理意义。 **推导方法**： - 传递函数可以通过对系统的微分方程进行拉普拉斯变换得到，如给出的例一、例二、例三和例四可能展示了不同的求解步骤和实例。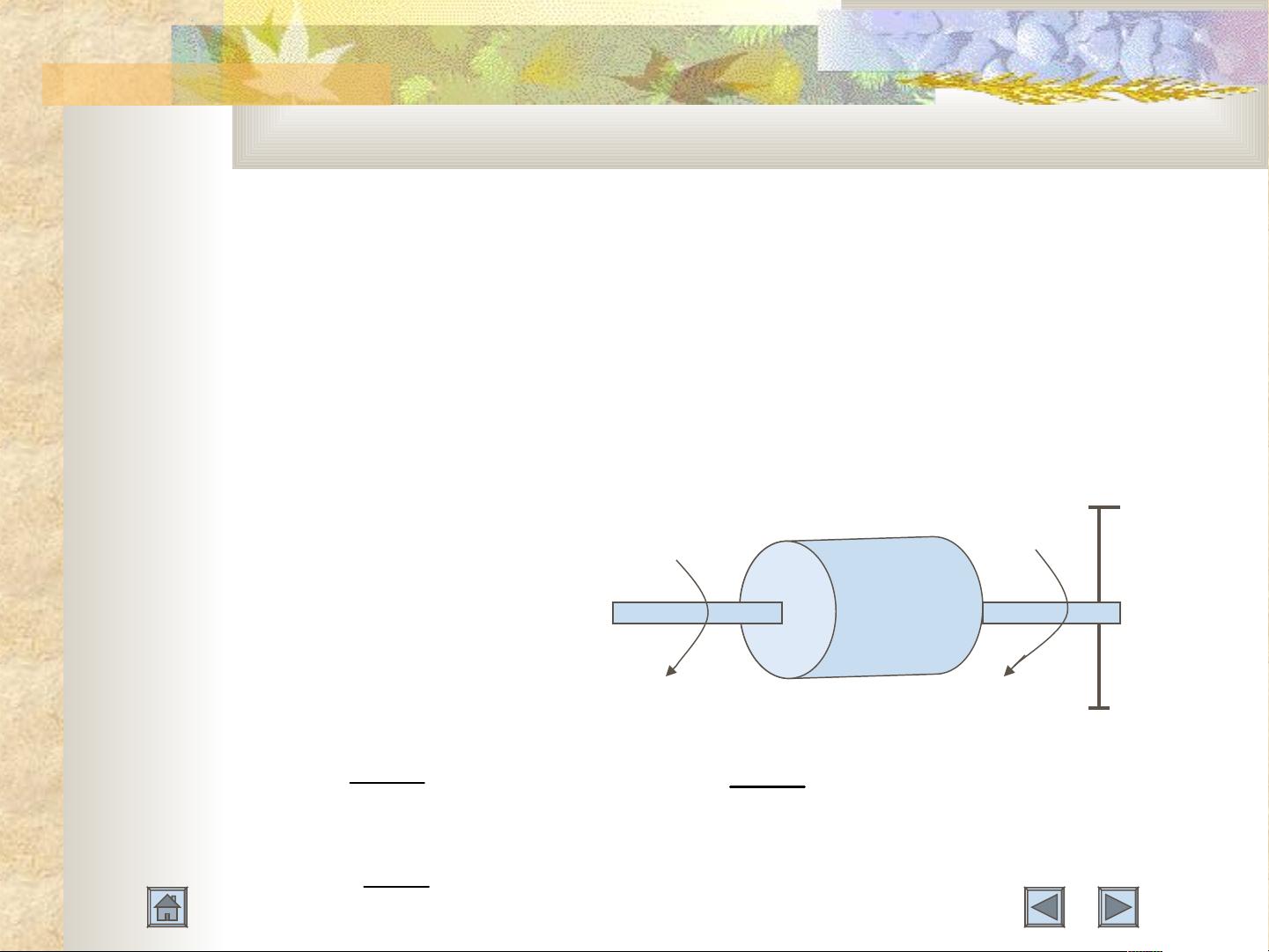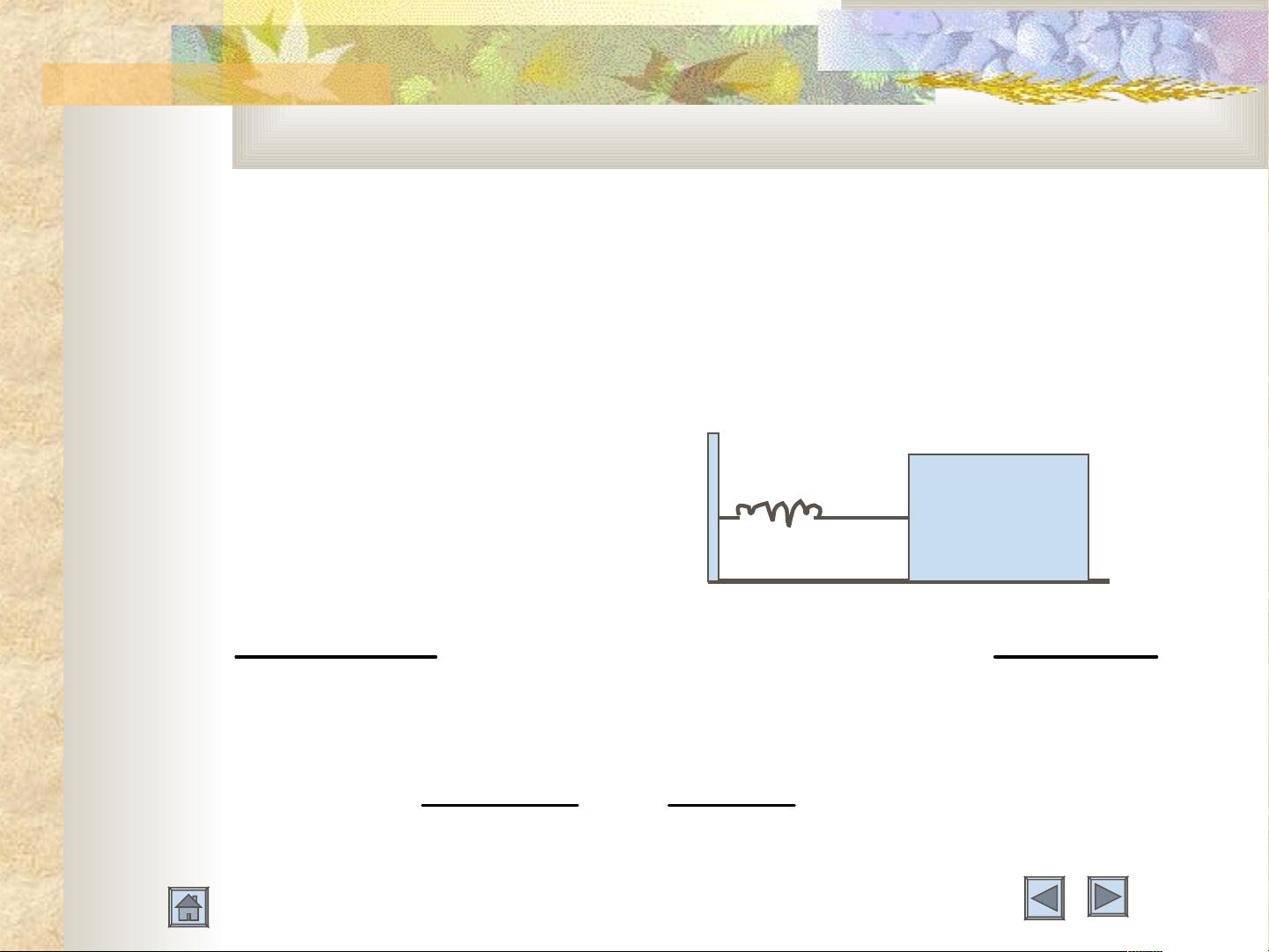 **应用**： - 在机械阻抗分析法中，传递函数被用来研究机械系统的动力学行为，比如弹簧-质量系统、惯性环节等，通过计算它们的传递函数来分析系统的响应。 - **典型环节**：理解了传递函数后，可以识别并分析各种典型环节，如积分环节、比例环节、惯性环节等，这些基本环节构成了许多复杂控制系统的基础。 掌握传递函数的概念、推导方法和其性质，对于理解并设计线性控制系统至关重要，它能够帮助工程师预测和优化系统的动态性能。在工程实践中，通过对系统传递函数的分析，可以评估系统稳定性、频率响应以及系统闭环控制性能。