一阶可控差分阵列麦克风不匹配影响分析：确定性和最坏情况

163 浏览量更新于2024-07-14 1 收藏 1.4MB PDF 举报

本文是一篇深入研究一阶可控差分阵列（First-Order Steerable Differential Array, FOSDA）在实际应用中遇到的麦克风不匹配问题的研究论文。FOSDA是一种特殊的声学阵列系统，它通过一个小型的四麦克风阵列结构，通过线性组合实现单极子和两个正交偶极子的响应，从而构建其方向性特性。麦克风不匹配是指阵列中各个麦克风的特性差异，这对阵列的整体性能有着显著的影响。论文主要关注两点：一是确定性分析，即探讨在给定的麦克风不匹配条件下，FOSDA的方向性因子（Directivity Factor, DF）如何精确计算和预测。方向性因子是衡量阵列指向性或能量集中度的重要指标，对语音增强、噪声抑制等应用场景至关重要。作者可能采用数学模型和信号处理技术来量化这种依赖于麦克风参数的DF变化。二是最坏情况分析，即分析当麦克风不匹配达到最大程度时，FOSDA的方向性性能可能出现的最大衰减或者失真。这有助于系统设计者了解在极端条件下的性能极限，以便采取措施进行优化或者提供稳健的设计策略。在确定性分析部分，作者可能会详细讨论如何通过系统的物理模型，如声学传输函数和阵列响应函数，结合统计参数（如麦克风灵敏度、相位延迟等）来确定DF的理论值。同时，可能会涉及到误差分析，以评估不匹配对DF估计的精度影响。在最坏情况分析方面，作者可能通过对麦克风不匹配的各种可能组合进行仿真或理论推导，找出使DF性能下降的最小和最大值。这可能包括对不匹配参数的敏感性分析，以及提出一些抗干扰措施，比如校准算法或者阵列设计优化。此外，论文还可能包含实验结果，通过实际测量验证理论分析，以展示在实际应用中的效果。论文最后会总结关键发现，并对未来研究方向提出建议，例如针对麦克风不匹配问题的补偿方法，或者针对其他类型差分阵列的研究。这篇论文为理解和处理一阶可控差分阵列在麦克风不匹配条件下的方向性挑战提供了重要的理论依据和技术指导，对于音频处理、声纳系统、语音识别等领域具有实际应用价值。

2329-9290 (c) 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.

This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 10.1109/TASLP.2015.2506269, IEEE/ACM

Transactions on Audio, Speech, and Language Processing

IEEE/ACM TRANSACTIONS ON AUDIO, SPEECH, AND LANGUAGE PROCESSING 4

Note that for small microphone gain errors, we have that

≈ 2 and ξ

≈ 2, which implies that ρ ≈ 2 and λ ≈ 4.

Consequently, (11) can be further reduced to

(g)

(Ω, α) ≈

24Ω

+ 3 (1 − α)

24Ω

+ 8Ω

(1 − α)

+ 3(1 − α)

. (15)

Specially, as expected, when there are no microphone gain

errors, it follows that (15) will degenerate to the DF of ideal

FOSDA, i.e., (7).

Regarding the effects of microphone gain errors on the DF

of the FOSDA, we have the following properties.

Property 3: The DF of the FOSDA with microphone gain

errors will always be greater than or at least equal to 1.

Moreover, the DF is equal to 1 if and only if α = 1.

Proof: See Appendix A.

Note from (3) that the FOSDA will degenerate into an

omnidirectional monopole when α = 1. Moreover, by (6),

it follows that the DF of an omnidirectional monopole or

omnidirectional microphone is equal to 1. Thus from Property

3, we know that the DF of the FOSDA will be no worse

than an omnidirectional microphone even in the presence of

microphone gain errors, i.e., we can always beneﬁt from using

the FOSDA instead of an omnidirectional microphone.

Property 4: The DF of the FOSDA with microphone gain

errors will decrease with frequency or array size decreasing.

Proof: It follows from inspection of (37) in Appendix A

that Q

(g)

(Ω, α) is an increasing function of Ω.

According to Property 4, the FOSDA is more sensitive to

microphone gain errors in low frequencies or for small-sized

arrays. This is similar to the effect of microphone mismatches

on the additive microphone arrays [22], [23].

Property 5: For the maximum value of the DF, it holds that:

1) The maximum achievable DF remains equal to 4 when

ζ = 0, i.e., when the gain errors of microphones M

and

are the same, and those of microphones M

and M

are the same.

2) For the general case ζ = 0, the maximum value of the

DF is always less than 4. In particular, when

α =

3ζ − 2



2Ω

(9ζ + 32Ω

) + 16Ω

3ζ

, (16)

the DF attains its maximum value given by

max

α∈[0,1]



(g)

(Ω, α)



≈

54Ω

+ 3Υ

6Ω

(2Υ − 3)

+ 8Ω

+ 3Υ

(17)

where Υ =

√

2Ω

(9ζ+32Ω

)−8Ω

Proof: See Appendix B.

Recall that the maximum value of the DF of ideal FOSDA

is equal to 4, which is achieved at α = 0.25 (hypercardioid

response). To keep the maximum achievable DF unaffected

by microphone gain errors regardless of mainlobe steering

direction, Property 5 indicates that the only means is to choose

sensors wisely such that each pair of diagonal microphones

have the same characteristics, i.e., η

= η

and η

= η

Otherwise, the maximum achievable DF will always degrade

due to microphone gain errors.

0 0.2 0.4 0.6 0.8 1

1.5

2.5

3.5

Case 1, simulation results

Case 1, theoretical results

Case 2, simulation results

Case 2, theoretical results

Case 2

Case 1

Fig. 3. DF vs. α with microphone gain errors, where φ

= 60

◦

, and

Ω = π/16. Case 1: η

= 0.9, η

= 0.93, η

= 1.1, η

= 1.04; and Case

2: η

= η

= 0.9, η

= η

= 1.04.

0.2

0.4

0.6

0.8

210

240

270

120

300

150

330

180

α=0.25

α=0.5

(a)

0.2

0.4

0.6

0.8

210

240

270

120

300

150

330

180

α=0.25

α=0.5

(b)

Fig. 4. Normalized array responses of the FOSDA with/without microphone

gain errors, where φ

= 60

◦

and Ω = π/16. (a) Ideal FOSDA. (b) With

microphone gain errors same as Case 1 in Fig. 3.

Now we present several numerical examples to support the

above deterministic analysis. Consider two cases of micro-

phone gain errors: 1) η

= 0.9, η

= 0.93, η

= 1.1,

= 1.04; and 2) η

= η

= 0.9, η

= η

= 1.04, i.e.,

the special case where the gain errors of microphones M

and M

are the same, and those of microphones M

and M

are the same. Herein, the mainlobe steering direction is set to

= 60

◦

, and Ω = π/16.

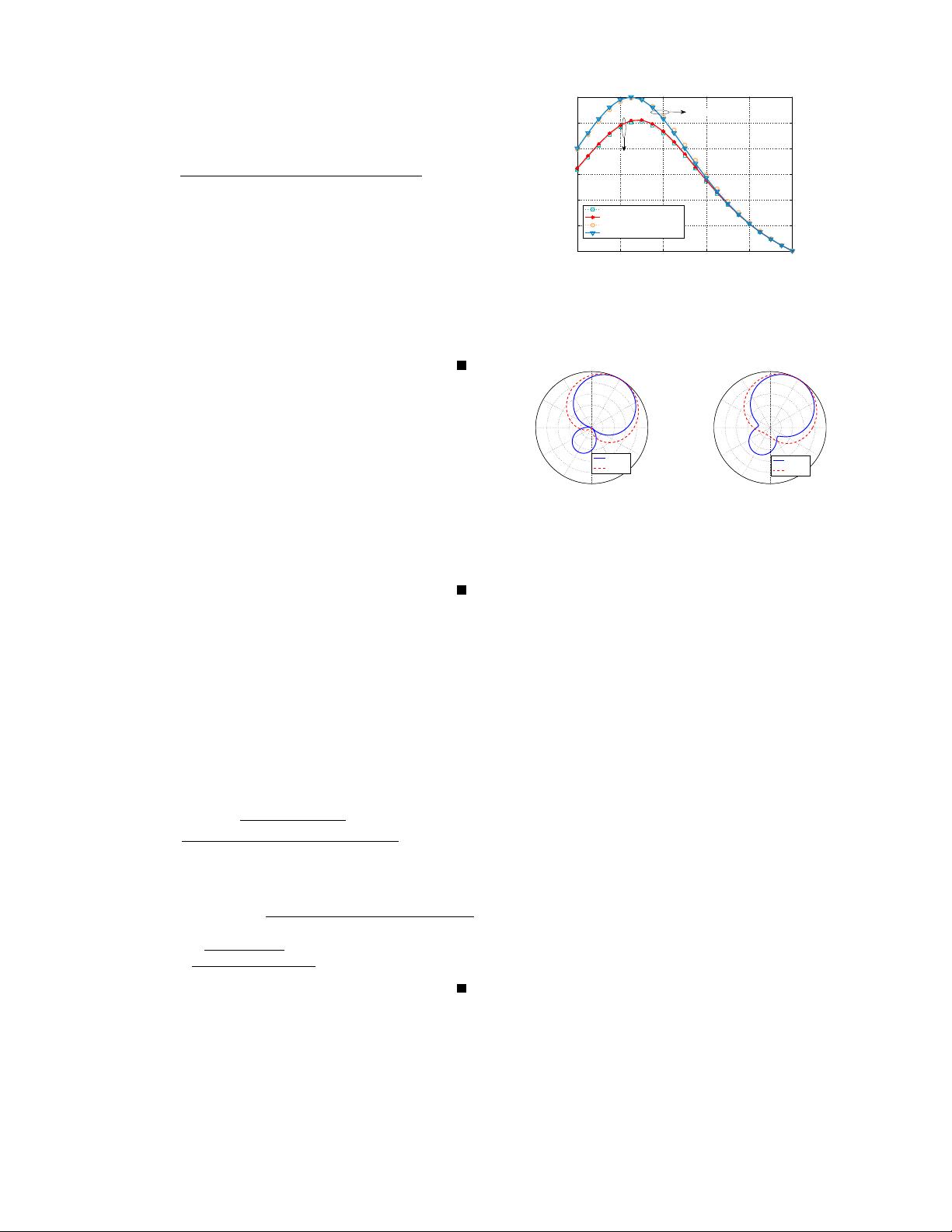
Fig. 3 shows the DF of the FOSDA versus α for the two

cases of microphone gain errors. Although some approxima-

tions have been used in our theoretical analysis, the theoretical

results are well-consistent with the simulation results, as

shown in Fig. 3. We can see from the simulations results

that the DF is always greater than 1 for arbitrary α ∈ [0, 1)

and equal to 1 only when α = 1, i.e., when the FOSDA

degenerates into a monopole, which is in agreement with

Property 3. Moreover, for Case 1, by Property 5.2 when

α = 0.280 the DF achieves its maximum value of 3.52.

This is very close to the simulation results where the DF

achieves the maximum value of 3.55 when α = 0.281. While

for Case 2, comparing with Fig. 2(a), i.e., the DF of ideal

FOSDA without microphone mismatches, we can see that the

microphone gain errors in such a case have little effect on

the DF of the FOSDA, which agrees well with our ﬁnding in

Property 5.1. Fig. 4(b) shows the normalized array responses

of the FOSDA with microphone gain errors as Case 1 in Fig. 3.

Note that the normalized array responses of the FOSDA with

microphone gain errors as Case 2 in Fig. 3 are actually same

as those of ideal FOSDA, i.e., Fig. 4(a). Comparing Fig. 4(b)

剩余16页未读，继续阅读

weixin_38726255

粉丝: 3
资源: 879

一阶可控差分阵列麦克风不匹配影响分析：确定性和最坏情况

一阶差分麦克风阵列双通道语音增强技术

掌握MATLAB实现线性差分麦克风阵列的差分波束成形

信号处理视角下的差分麦克风阵列设计与性能分析

一阶可控差分麦克风阵列的指向性因子

基于matlab使用差分波束成形技术形成线性差分麦克风阵列

声功率方向性分析：根据球坐标上的声压计算声功率并分析声源方向性。-matlab开发

麦克风阵列

BeanForming.zip_beanforming_差分波束形成_差分阵_波束图_麦克风阵列

麦克风阵列语音增强技术：基于波束形成法的研究

基于改进LSA-MMSE的麦克风阵列语音增强算法：提升信噪比与稳定性

最新资源