五自由度机械臂D-H法运动学解析
版权申诉
"五自由度机械臂的运动学分析,包括正向运动学、逆向运动学和机器人模型建立。"
在机械臂的设计与控制中,运动学是研究其运动特性的关键部分。五自由度机械臂具有五个独立的关节,能够实现复杂的空间运动。本文主要围绕机械臂的正向运动学、逆向运动学以及机器人模型的建立展开讨论。
1. 正向运动学分析
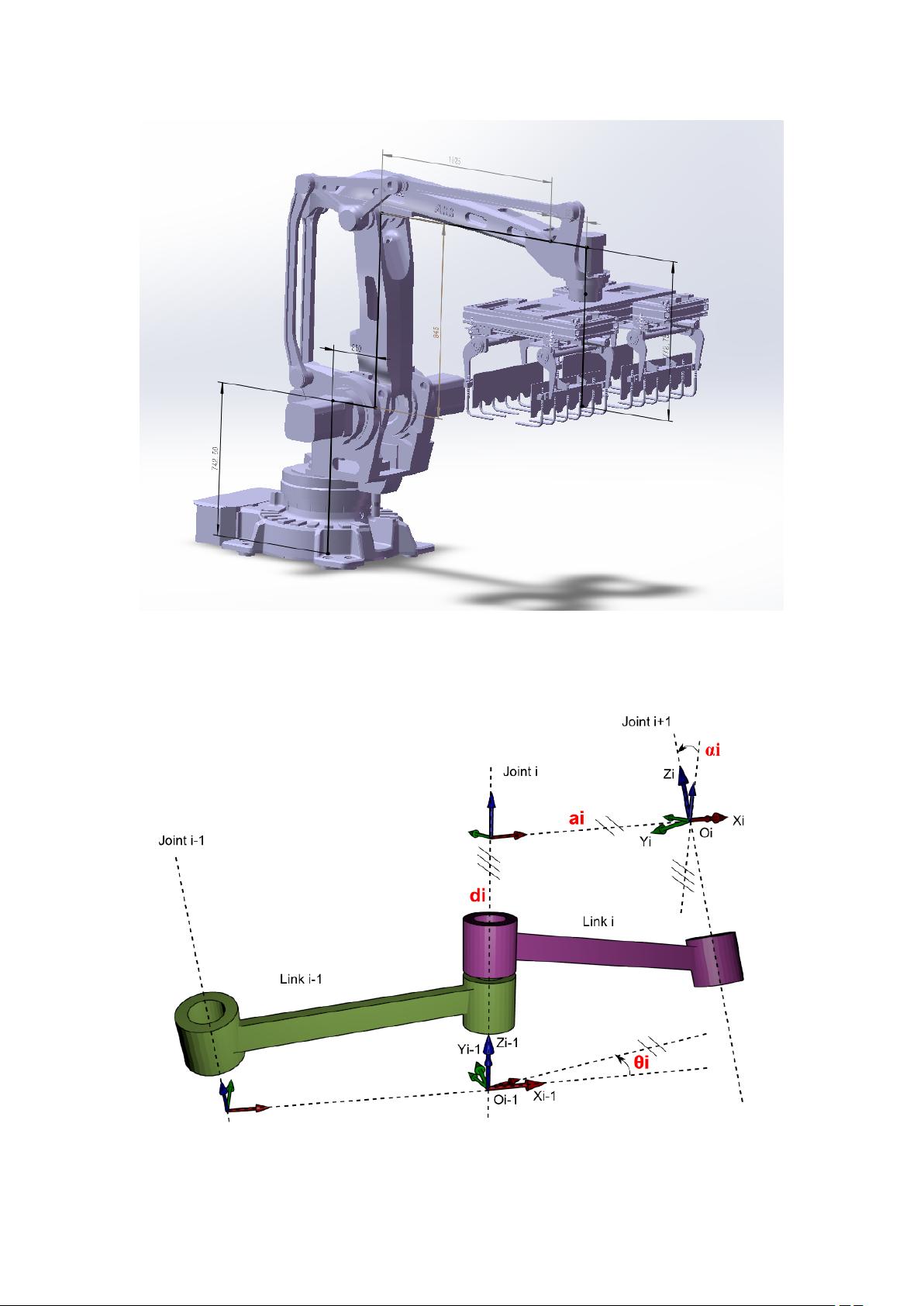
正向运动学是确定机械臂末端执行器位置和姿态的过程,通常采用D-H(Denavit-Hartenberg)参数法来建模。D-H参数包括关节角(theta)、关节轴之间的距离(d)、关节轴相对于前一关节的偏移角度(alpha)以及相邻两连杆之间的相对旋转角度(theta)。通过这些参数构建的变换矩阵描述了机械臂中各个关节之间的相对位姿。在MATLAB中,可以编写函数`trans`计算变换矩阵,然后通过串联这些矩阵得到从基座到末端执行器的整体变换矩阵`T05`,从而得出末端执行器的位置和方向。
2. 逆运动学分析
逆向运动学则是给定末端执行器的位置和姿态,反推出各关节角的值。这里,我们面临的是一个非线性方程组,通常需要通过迭代方法求解。首先对正向运动学方程进行操作,将得到的方程除以特定项,然后通过比较方程的特定元素来解出关节角。在给定的示例中,通过对方程进行一系列操作并连续乘以各关节变换矩阵的逆,可以逐步求得关节角的值。
3. 机器人模型建立
建立机器人的三维模型是验证其运动学分析的重要步骤。在MATLAB的Robotics Toolbox中,可以通过`Link`和`SerialLink`函数创建并连接各个连杆,模拟机械臂的结构。`Link`函数用于创建单个连杆,而`SerialLink`函数用于串联这些连杆以构建整个机械臂模型。在这个过程中,需要提供每个连杆的长度、关节类型(旋转或移动)以及相应的关节参数。
总结起来,五自由度机械臂的运动学分析涉及从关节变量到末端执行器位置的映射(正向运动学)以及从末端执行器位置到关节变量的映射(逆向运动学)。此外,借助MATLAB的Robotics Toolbox,可以实现机械臂的动态模拟,这对于理解和优化机械臂的设计与控制至关重要。通过深入理解这些概念,可以有效地应用于工业自动化、服务机器人等领域。
2368 浏览量
202 浏览量
1889 浏览量
点击了解资源详情
1336 浏览量
270 浏览量
231 浏览量
1713 浏览量
CAE工作者
- 粉丝: 225
最新资源
- 初学者入门必备!Visual C++开发的连连看小程序
- C#实现SqlServer分页存储过程示例分析
- 西门子工业网络通信例程解读与实践
- JavaScript实现表格变色与选中效果指南
- MVP与Retrofit2.0相结合的登录示例教程
- MFC实现透明泡泡效果与文件操作教程
- 探索Delphi ERP框架的核心功能与应用案例
- 爱尔兰COVID-19案例数据分析与可视化
- 提升效率的三维石头制作插件
- 人脸C++识别系统实现:源码与测试包
- MishMash Hackathon:Python编程马拉松盛事
- JavaScript Switch语句练习指南:简洁注释详解
- C语言实现的通讯录管理系统设计教程
- ASP.net实现用户登录注册功能模块详解
- 吉时利2000数据读取与分析教程
- 钻石画软件:从设计到生产的高效解决方案