深入理解SVM:从八股简介到核心概念解析
需积分: 10 112 浏览量
更新于2024-07-29
1
收藏 560KB PDF 举报
"这篇资源是一个关于SVM(支持向量机)的入门教程,旨在帮助初学者快速理解和进入SVM的世界。SVM是由Cortes和Vapnik在1995年提出的,尤其适用于小样本、非线性和高维模式识别任务,并可应用于函数拟合等其他学习问题。该教程基于统计学习理论的VC维理论和结构风险最小化原则,旨在寻找最佳的模型复杂性和学习能力之间的平衡,以提高模型的泛化能力。"
在深入探讨SVM之前,我们需要了解一些基本概念。Vapnik是统计机器学习领域的权威,他的著作《Statistical Learning Theory》阐述了统计机器学习的核心思想,即通过理论分析预测模型的性能,而传统机器学习则更多依赖于实践和经验。
VC维是衡量函数类复杂度的一个指标,它可以看作是问题的复杂性度量。SVM的优势在于其对VC维的关注,即使面对高维样本,SVM也能有效地处理,这得益于核函数的引入,使得SVM在处理如文本分类这样的高维数据时表现出色。
结构风险最小化是SVM优化目标的关键概念。在机器学习中,我们通常需要找到一个近似模型(假设)来逼近未知的真实模型。由于真实模型无法直接获取,我们只能通过选择使得模型与真实解差距尽可能小的假设。结构风险最小化就是寻找这种差距最小化的策略,它在训练过程中权衡模型复杂性和泛化误差,以避免过拟合或欠拟合,从而提高模型在未见过的数据上的表现。
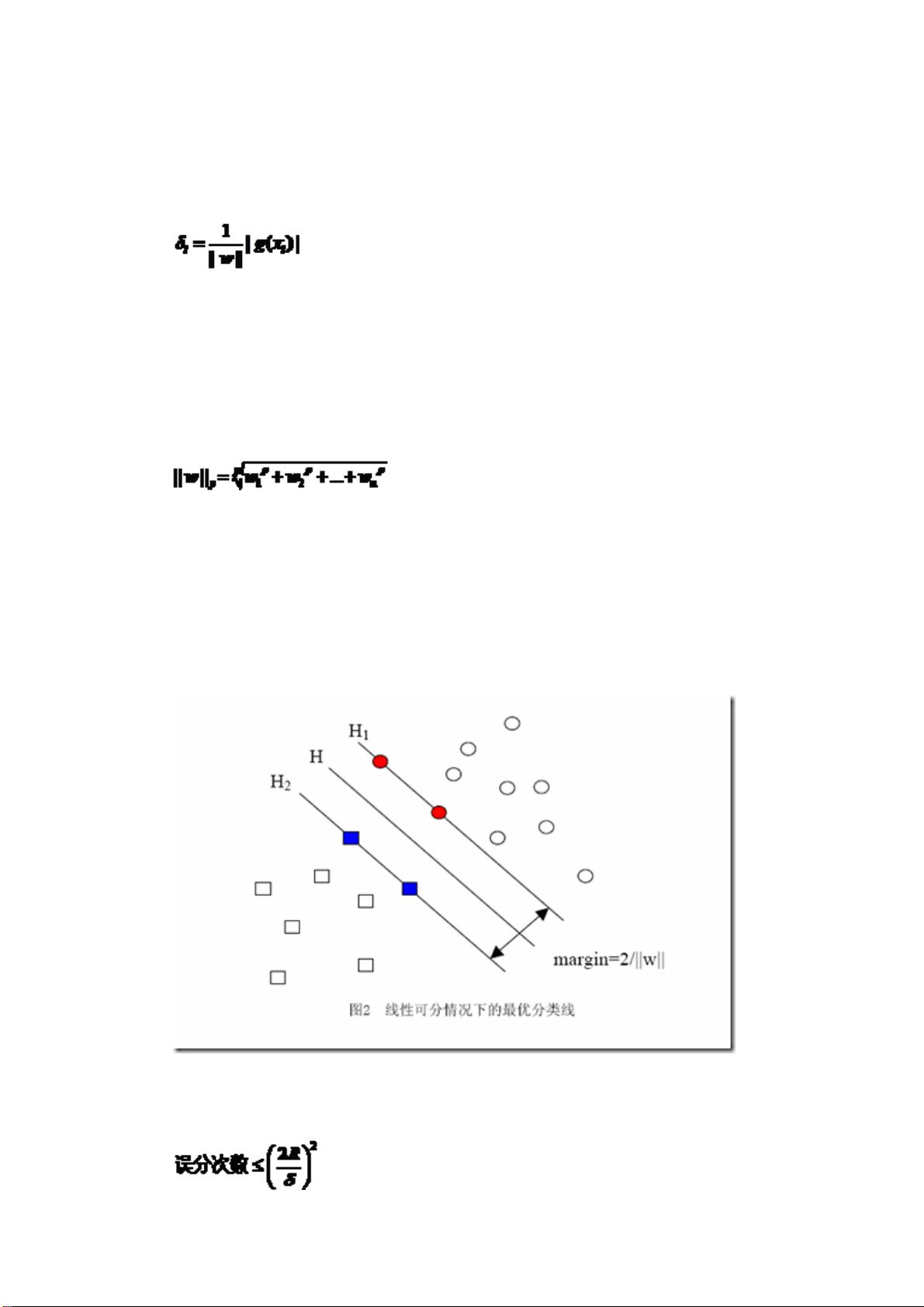
SVM的核心算法是最大间隔分类,它的目标是在训练数据中找到一个最优超平面,这个超平面能够最大程度地将不同类别的样本分开。通过使用核函数,SVM能够将数据映射到高维空间,使得原本在低维空间难以分离的非线性数据变得容易线性可分。
在实际应用中,SVM可用于分类和回归任务,特别是在生物信息学、文本分类、图像识别等领域有广泛的应用。此外,SVM还可以与其他机器学习技术结合,例如集成学习,以提升模型的整体性能。
SVM是一个强大且灵活的机器学习工具,其理论基础深厚,实践效果显著。通过深入学习和理解SVM的基本原理和实践技巧,你将能够掌握这个强大的分类和回归方法,为你的数据分析和预测项目提供有力支持。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2010-11-24 上传
2010-03-12 上传
2010-11-05 上传
2010-04-28 上传
2012-07-02 上传
散木振东
- 粉丝: 1
- 资源: 7
最新资源
- Elasticsearch核心改进:实现Translog与索引线程分离
- 分享个人Vim与Git配置文件管理经验
- 文本动画新体验:textillate插件功能介绍
- Python图像处理库Pillow 2.5.2版本发布
- DeepClassifier:简化文本分类任务的深度学习库
- Java领域恩舒技术深度解析
- 渲染jquery-mentions的markdown-it-jquery-mention插件
- CompbuildREDUX:探索Minecraft的现实主义纹理包
- Nest框架的入门教程与部署指南
- Slack黑暗主题脚本教程:简易安装指南
- JavaScript开发进阶:探索develop-it-master项目
- SafeStbImageSharp:提升安全性与代码重构的图像处理库
- Python图像处理库Pillow 2.5.0版本发布
- mytest仓库功能测试与HTML实践
- MATLAB与Python对比分析——cw-09-jareod源代码探究
- KeyGenerator工具:自动化部署节点密钥生成