揭秘傅里叶级数：从叠加原理到频域构建

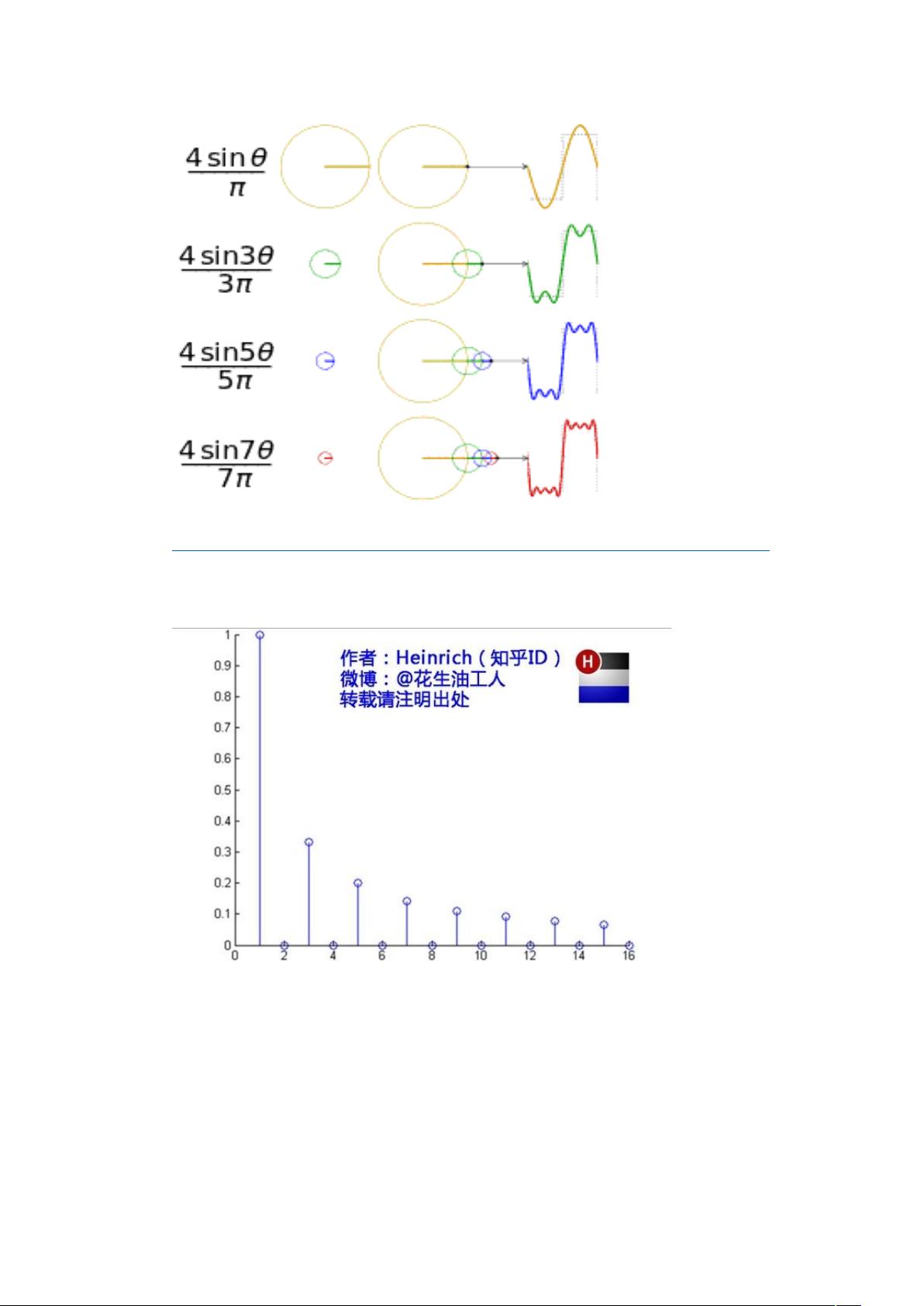
傅里叶级数是一种数学工具，用于将任何周期性函数分解为一组简单正弦或余弦函数的线性组合，即无限多个频率成分的叠加。这个概念最初由法国数学家约瑟夫·傅里叶提出，因此得名。它是信号处理、电子工程、物理学等领域中的核心原理，特别是在分析周期性信号的频谱分析中发挥着重要作用。 首先，傅里叶级数的核心思想是通过有限数量的正弦波（或余弦波）的叠加来模拟复杂的波形。例如，开始时提到的例子是将正弦曲线波叠加以形成矩形波。通过逐步增加正弦波的数量，我们可以看到这些波的相位变化和振幅调整如何协同作用，最终达到目标波形。这个过程体现了数学上的收敛性，尽管看似无穷多的正弦波组合在实际应用中可能只需有限数量就可以达到足够精确的近似。 每个正弦波都有其特定的频率和振幅，其中频率决定了波形的周期性，而振幅则决定了波形在某一时刻的高度。正弦波可以被理解为周期性圆周运动在直线上投影的结果，这使得频率分量与二维坐标系中的周期和振幅相对应。在频域中，基本单元就是频率，频率为1的正弦波cos(t)代表了一个基本的周期性单位，而频率为0的直流分量（如cos(0t））表现为一条直线，它不随时间变化，只影响波形的整体位置。 傅里叶级数中的“1”和“0”频率分量是构建频域分析的基础，它们分别对应于周期性和静态成分。在实际应用中，傅里叶变换技术被用来计算信号的频谱，揭示信号中的频率成分及其强度，这对于噪声过滤、信号恢复、通信系统设计等有着广泛的应用。 总结来说，傅里叶级数是解析周期性信号的重要工具，它揭示了信号复杂性的内在结构，并通过分解为简单的正弦波来简化处理。理解和掌握傅里叶级数有助于深入理解信号的动态特性和频域表示，是任何从事相关领域工作的人必须掌握的基础知识。